본 글에서는 ARIMA 모형을 활용해 미래 미국채 Spread 추이를 continuous하게 예측하고, 이어서 Probit 모형을 통해 ARIMA 예측값을 경기침체 여부로 변환한다. 경제 예측 모델링을 수행할 때에는 가급적 단순한(파라미터가 적은) 모델, 해석가능한 모델을 사용하는 것이 좋다. 일반적인 인식과 달리 경제 데이터는 딥러닝과 같은 모델 아키텍처로 적합시킬 만큼 대용량이 아닐 뿐더러 제대로 적합되지 않았을 때 Fat Tail Risk가 미치는 영향이 치명적일 수 있기 때문이다.
따라서 시계열 모델 파라미터를 분리 해석할 수 있는 ARIMA 모형, 종속변수가 binary(이진) 변수일 때 yes or no 에 대한 발생 확률을 가장 단순하게 설명가능한 Probit 모형을 사용하고, 이를 통해 현재의 미국채 Spread로 미래 경기침체 향방을 추정 시도해보려 한다.
Step 1. 데이터 수집 및 전처리
먼저 FRED API에서 미국 장단기 금리(10년물, 2년물) 데이터, 그리고 Recession(경기침체) Indicator 데이터를 불러온다. Recession Indicator Ticker는 USREC이며, 아래 이미지와 같이 지난 연도별 경기침체 여부를 1 or 0으로 기록하고 있다.


ARIMA 모형으로 금리차를 예측할 것이므로 모델 입력값으로 넣을 spread를 계산한다. 계산한 장단기 금리 spread와 역사적 recession 시계열은 아래 차트에서 확인할 수 있다. (연도별 recession 여부는 red-flag로 표시해 두었다.)

스프레드 역전 시기 직후에는 항상 불황이 이어졌고, 다가올 2025년에도 동일한 상황이 반복될 수 있다.
Step 2. 금리 스프레드 시계열 패턴 분석
ARIMA 모델링을 수행하기 위해서 시계열 인자(입력 변수)는 정상성(Stationarity)을 만족해야 한다. 정상성은 시점에 따라 분포 통계(평균, 분산)가 변하지 않는 상태를 의미하며, 이것이 변한다면 분포의 영속성을 전제로 하는 통계 분석은 불가하다.
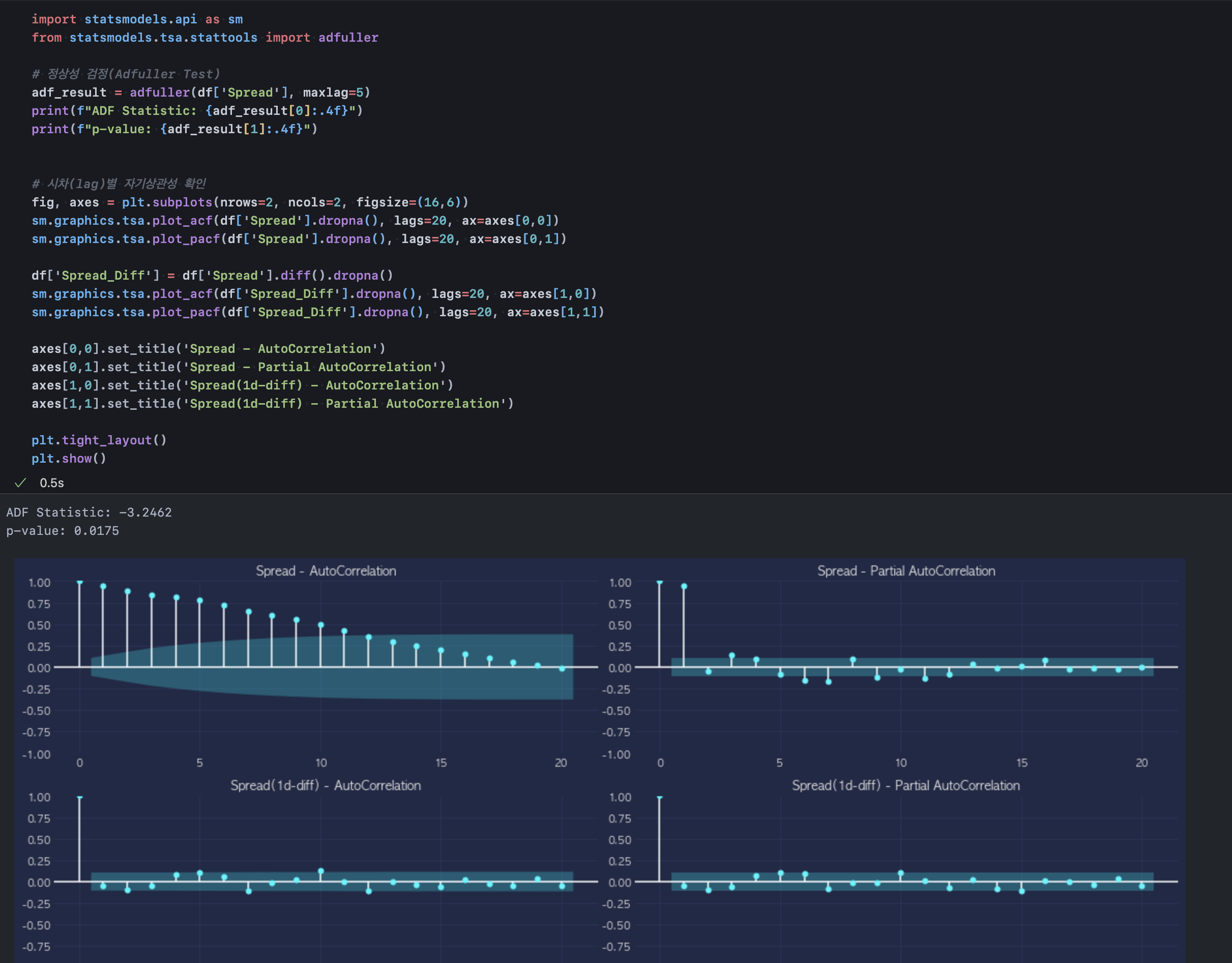
정상성 검정(ADF Test) 결과 p-value가 보편적인 significance level(유의 수준) 보다 낮다. 이에 "단위근이 존재한다"라는 ADF Test 귀무가설을 기각할 수 있다. 단위근이 존재하지 않으면 정상시계열일 가능성이 높지만 항상 그런 것은 아니다. ADF Test는 전체 시계열의 통계적 특성을 검사하므로 단위근으로 인한 단기적인, 약한 자기상관성은 발견해 내기 어려울 수 있다.
따라서 위와 같이 자기상관성, 부분자기상관성을 차트로 확인해 볼 필요가 있다. 그 결과 Spread의 시차별 Correlation을 보여주는 첫 번째 행에서 직전연도의 스프레드가 당해연도 스프레드와 매우 높은 상관성이 존재함을 알 수 있었다.
이렇게 자기상관성이 존재하는 시계열은 시차에 따라 통계적 분포를 달리하므로 예측 모형의 추론을 어렵게 만든다. 이 경우 2가지 선택지가 존재한다. 차분을 수행한 다음 정상시계열로 만들고 예측하거나, 자기상관성을 고려한 모델링을 수행하는 것이다.
Step 3. ARIMA 기반 금리 스프레드 예측
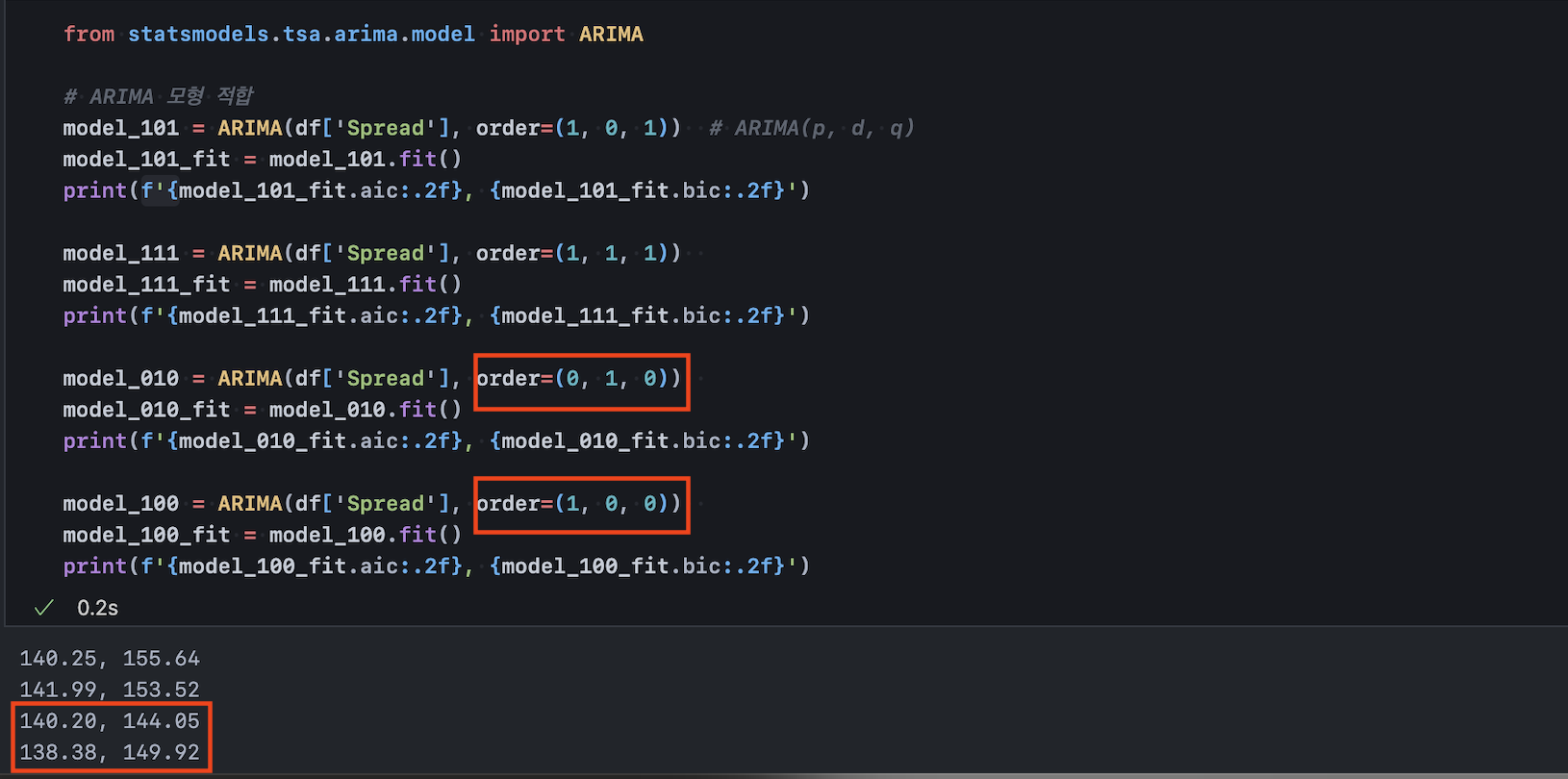
ARIMA 모형은 AR(p)+I(d)+MA(q)로 구성되고, p, d, q는 각각 자기상관성이 존재하는 차수, 모델 적합을 위해 필요한 차분 수, 오차연관성이 존재하는 차수를 의미한다. 각 인자를 유효 범위 내 다르게 설정하여 적합한 ARIMA 모델의 aic, bic 지표를 보면 앞서 언급한 선택지 2가지, 그러니까 차분을 수행한 다음 예측(p=0, d=1, q=0) 하거나 자기상관성을 고려한 모델링을 수행(p=1, d=0, q=0) 한 결과 trade-off가 존재함을 확인할 수 있다. aic(akaike information criterion)와 bic(bayesian information criterion)는 모델이 잘 적합했는가를 보여주며, 수치가 낮을수록 좋다.
다만, 모델 파라미터(p+q+intercept)를 과하게 쓰면 aic는 낮아질지라도 bic는 그렇지 않은데, bic는 과최적화 가능성을 마이너스 요소로 취급해 주기 때문이다. 따라서 두 지표(aic, bic) 사이 밸런스를 같이 보면서 '최소한의 파라미터로 최대한의 적합을 이루었는가?'를 평가해야 한다.
model_010의 경우 파라미터를 사용하지 않았고(*차분은 모델 파라미터로 취급하지 않는다), model_100은 1개의 파라미터(q=1)를 사용했다. 1차 자기상관성을 고려한 모델 적합을 수행하였고, 파라미터를 사용하지 않은 model_010 대비 bic는 높지만 전체 모델 중 aic가 가장 낮다. 잘 적합된 것이다.
여기서, model_010을 선택하지 않는 이유는 model_100보다 높은 aic 수치도 있지만 차분을 수행함으로 인해 정보손실이 발생하는 것을 피하려는 의도도 있다. 우리는 경제 예측 모형을 만들고 있고, 금리 스프레드의 경우 과거(전월, 전년도)가 현재(당월, 당해연도) 스프레드에 영향을 주는 추세적 움직임이 반드시 존재하기 때문에 이러한 움직임을 모델에 녹여내는 것이 합리적이다. 또한, 앞서 정상성 검정을 수행했을 때 자기상관성이 존재하긴 하나 전체 기간에 대해 비정상 시계열로 보기도 어렵기 때문에 일정 범위 내 통계분포가 유지되는 특성 역시 고려해 굳이 차분을 수행하지 않겠다.
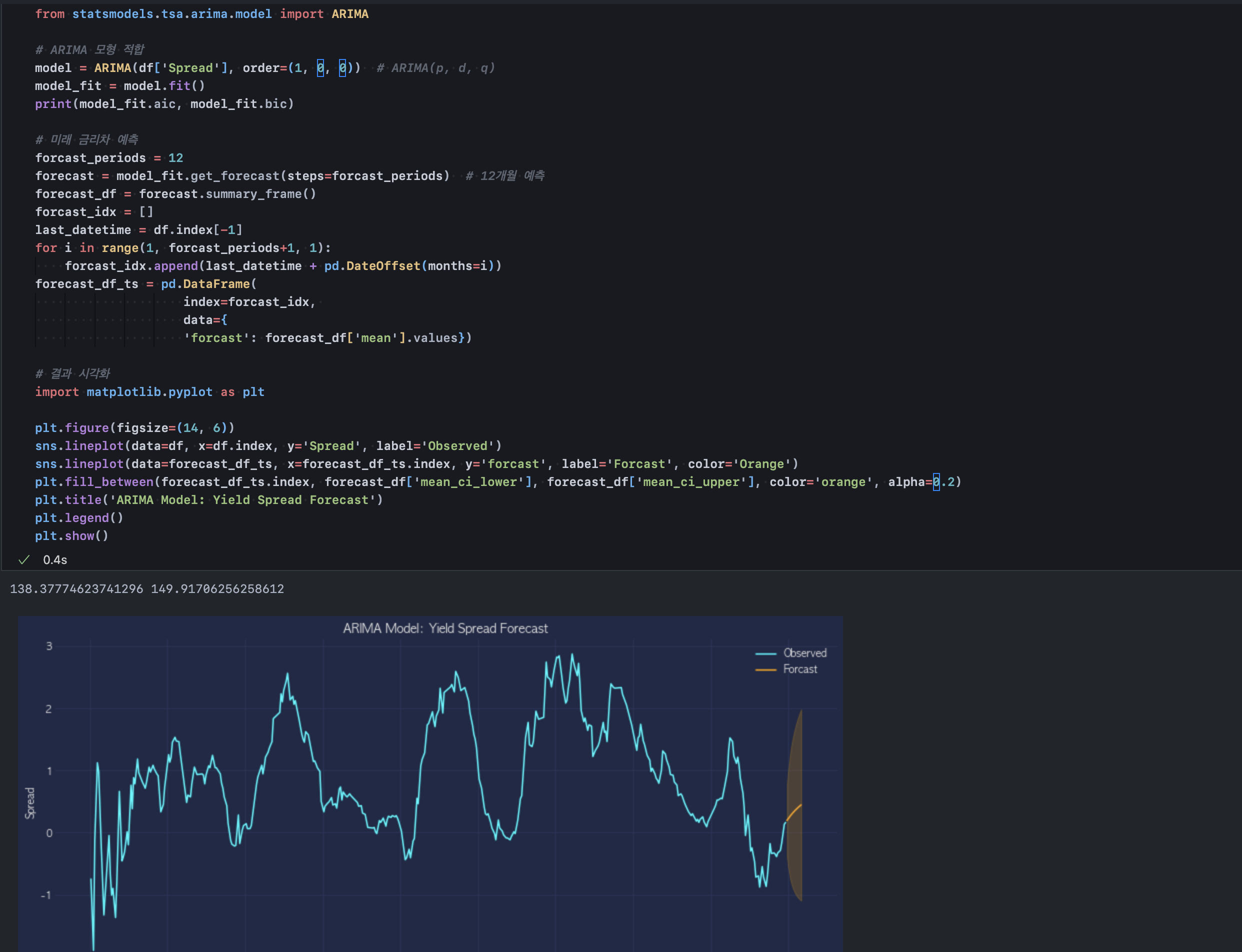
위 결론을 토대로 ARIMA(1,0,0) 모형에 과거 데이터를 적합시키고, 미래 12개월 금리 스프레드를 예측하였다. 신뢰구간이 넓긴 하나 전통 계량통계 모형의 한계로 인식하고, 이 범위 내 개별 시나리오를 구상해야 한다. 모형은 현실을 굉장히 축소한 형태이므로 경제 이론이나 현실 사건에 근거하지 않은, 단순히 모델의 추정치에만 의지하는 것으로는 효용을 얻기 어렵다.
Step 4. Probit 기반 경기침체 확률 예측
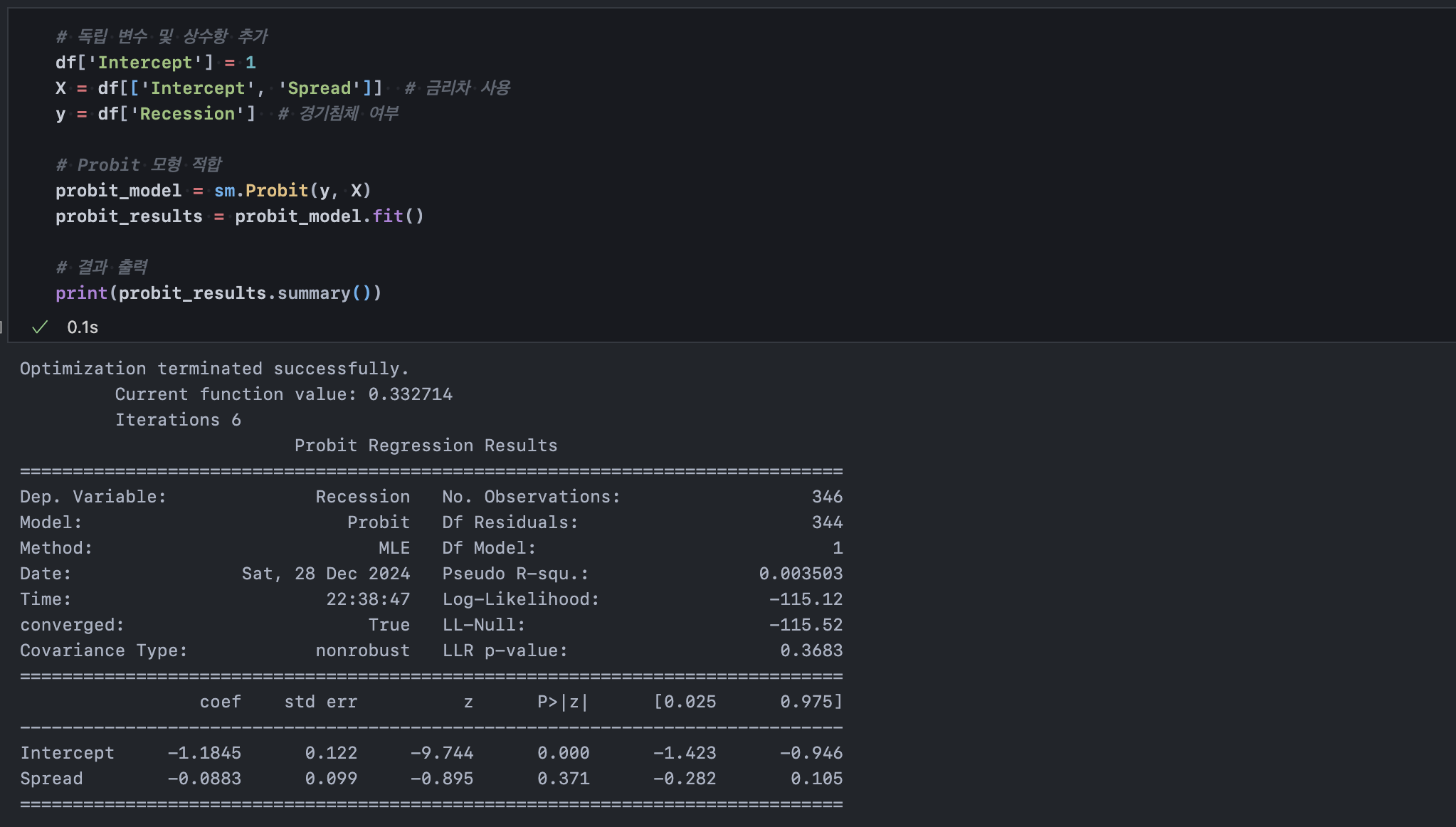
이제 ARIMA로 예측한 미래 12개월 금리 데이터를 다시 Probit 모형에 적합시키고, recession 여부를 예측해보려 한다. 그전에 Probit 모형이 spread 단일 변수만으로 recession에 대한 유효한 예측 효용을 가질 수 있는가?를 확인했다.
위 Probit Regression Results에서 coefficient table을 보면 Spread 변수의 coefficient가 -0.08로, Spread가 증가하면 recession 확률이 낮아질 것으로 예상할 수 있다. 그러나 해당 변수의 P-value가 0.371로, -0.08이라는 계수는 통계적으로 유의하지 않다. 따라서 spread 단일 변수로 recession을 예측하기에 Probit 모형이 충분히 적절하진 않은 것으로 보인다.
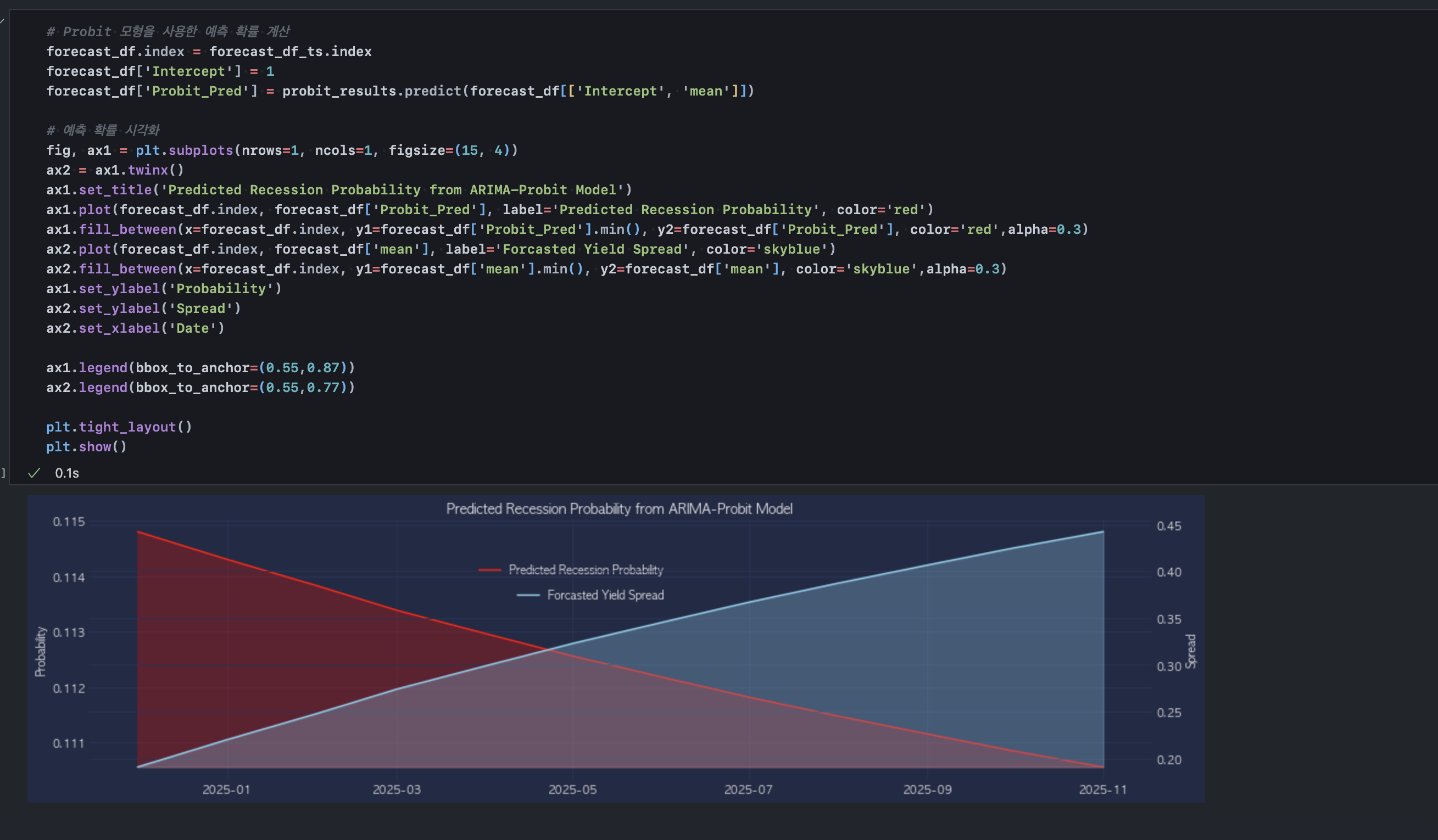
모형에서 Spread 변수의 계수는 음수이므로, 입력-출력 간에 반비례 경향성을 보인다. ARIMA(1,0,0)는 2025년 1월부터 해당 연도 연말까지 스프레드는 점차 증가할 것으로 예측했고, 이에 따라 Probit 회귀 모형은 Recession 리스크가 감소할 것으로 예측했다.
또, 모형 추정 결과로 볼 때 Recession 리스크 자체가 아주 높은 수준은 아닌데, 과거 시계열에서 recession 직전 장단기 스프레드 역전이 항상 발생했던 것을 고려하면 모델의 추정치를 온전히 신뢰하기는 어렵다. (*Probit 모형은 내부적으로 z-score로 1차 추론 결과를 얻고 이를 CDF 함수를 사용해 확률값으로 변환해 준다. 2025년 1월부터 11월까지 11% 수준의 불황 리스크가 존재한다고 해석할 수 있다.)
Step 5. 결론 / 인사이트
장단기 금리차는 역사적으로 유효한 경기 선행 지표로 활용될 수 있다. 이에 ARIMA 모형으로 미래 금리차를 1차 예측하고 예측된 금리차를 Probit 모델을 통해 경기침체 확률로 2차 예측했다.
Probit 모형으로 과거 금리 스프레드와 경기 불황 지표를 적합시켰을 때 두 지표는 서로 약한 반비례 관계를 갖고 있으며 2025년 금리 스프레드가 높아질 것이라고 예측한 ARIMA 모형 추정 결과에 따라 Probit 모형은 경기 불황 가능성이 점차 낮아질 것으로 예측하고 있다.
그러나 모델 추정 결과에 대한 통계적 유의성이 낮은 수준이므로 이러한 모델링 방법론을 투자에 직접 활용하기보다 경제적 근거와 추가 정량적 지표를 활용하여 의사결정 보조 수단으로 참고하는 정도가 적절하겠다.