1. Core CPI 개요 및 BIS API 사용법
근원 소비자물가지수는 기존 소비자물가지수(CPI)에서 외부 공급 충격 요인이 될 수 있는 식품과 에너지 부문을 제외한 지수다. 미국의 월별 소비자 가격 변동을 보여주는 대표 지수이므로 글로벌 인플레이션 수준을 가늠하고 연준의 금리 정책을 전망하는 단서가 된다.
미국 노동통계국이 운영하는 U.S. BUREAU OF LABOR STATISTICS에서는 CPI를 포함해 여러 글로벌 경제 지표를 API로 제공하고 있으며 파이썬 requests 모듈로 간단히 필요한 데이터를 호출할 수 있다.

중요한 부분은 requests.post()의 인자로 던져주는 data다. 지표 코드(seriesid)와 수집할 기간(startyear, endyear)을 json 형식으로 입력해야 한다. 그럼 지표 코드는 어디서 확인할 수 있을까?
BIS는 대중적으로 사용되는 지표들을 Top Picks로 모아서 보여주고 있다. 네비게이션 바에서 DATA TOOLS > Data Retrieval Tools > BLS Popular Series를 선택하면 다음과 같은 페이지가 표시된다.

크게 고용, 생산성, 가격, 급여(보수)라는 4개의 카테고리로 제공하고 있다. Price Indexes 부문 중 CPI-U/Less Food and Energy (Unadjusted)가 우리가 찾는 데이터다.

지표에 대한 설명은 월간 리포트를 통해 상세히 확인할 수 있다. 검색창에 cpi 등을 입력하거나 ECONOMIC RELEASES 탭의 Latest Releases를 클릭하면 자료들이 유형별로 리스트업 된다.


2. Core CPI 데이터 추출 및 집계
CPI는 기본적으로 전년 동월 대비 성장률을 본다. 특히 올해의 인플레이션이 작년 대비 어느 수준인가?를 확인하려면 먼저 YoY(전년 대비 증감)를 집계하고 이후 분석 필요에 따라 전월 대비 증감을 체크한다.
데이터 추출부터 YoY 집계까지의 파이썬 코드는 다음과 같다.
def get_time_idx(x):
if x['month'] <= 9:
date = f"{x['year']}-0{x['month']}"
else:
date = f"{x['year']}-{x['month']}"
return date
def get_data(json_data):
df = pd.DataFrame(json_data['Results']['series'][0]['data']).iloc[:,[0,1,2,4]]
df['month'] = df['period'].apply(lambda x : int(x[1:]))
df.drop(columns=['period'], inplace=True)
df['date'] = df.apply(lambda x : get_time_idx(x), axis=1)
df.drop(columns=['year','periodName','month'], inplace=True)
df = df.sort_values(by='date').set_index('date')
df['value'] = df['value'].astype('float64')
df['yoy'] = df['value'].pct_change(periods=12)
df = df.dropna()
return df
headers = {'Content-type': 'application/json'}
data = json.dumps({"seriesid": ['CUUR0000SA0L1E'],"startyear":"2015", "endyear":"2023"})
p = requests.post('https://api.bls.gov/publicAPI/v2/timeseries/data/', data=data, headers=headers)
json_data = json.loads(p.text)
df = get_data(json_data)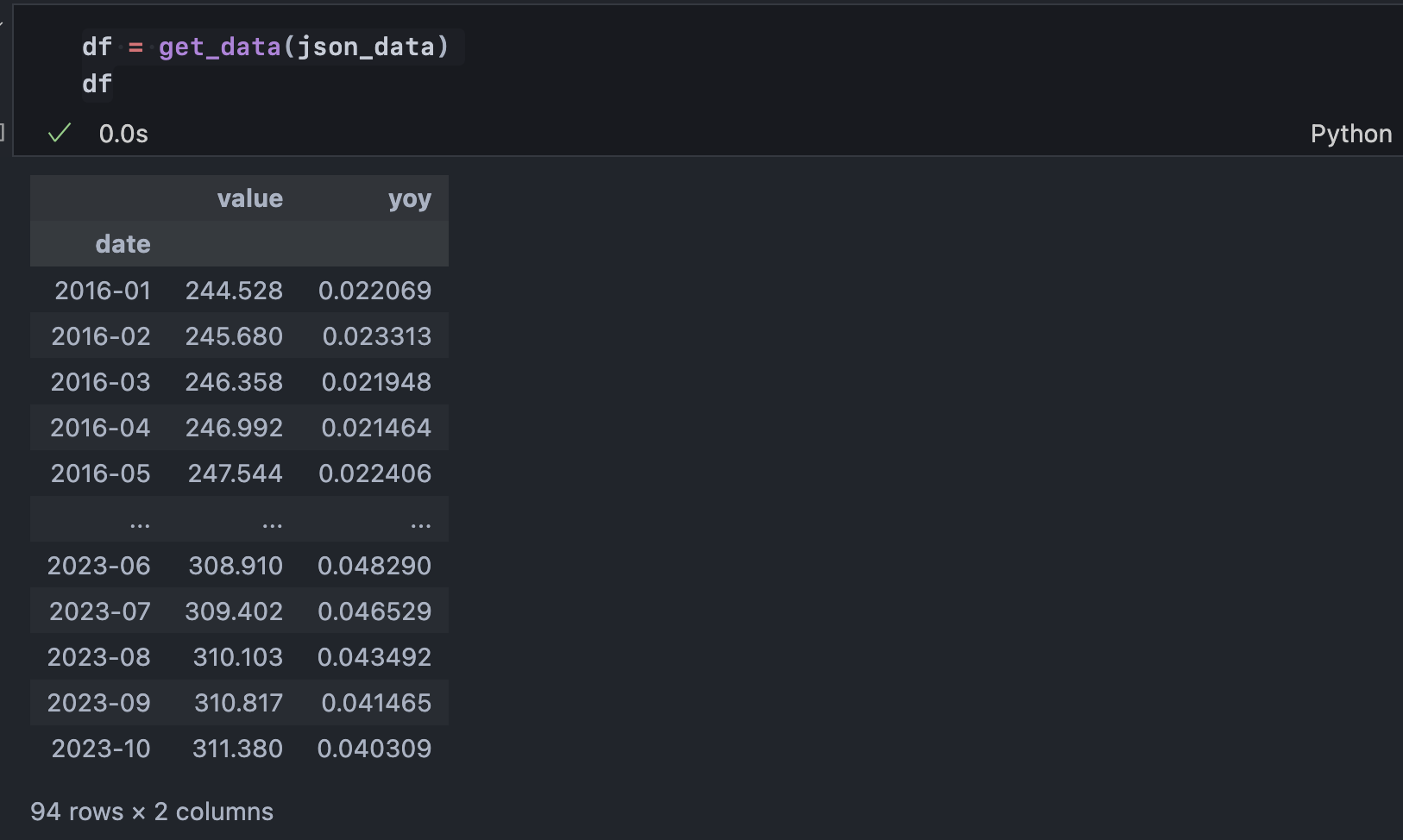
컬럼 중 value는 원본 데이터, yoy는 전년 동월 대비 증감이다. 여기서 각각 다시 직전 월 대비 증감을 구할 수 있으며 해석하자면 소비자물가지수가 전월 대비 얼마나 성장했는가? 소비자물가지수의 전월 동월 대비 증감률이 전월 대비 얼마나 성장했는가?이다.
코로나 전후 각 데이터의 양상을 보면 그 차이를 가시적으로 확인할 수 있다.
fig, axes = plt.subplots(ncols=1, nrows=4, figsize=(6,10))
event_idx = df.index.to_list().index('2020-01')
df['value'].plot(ax=axes[0])
axes[0].axvline(x=event_idx, c='pink', linestyle='--', linewidth=0.7)
df['value'].diff().plot(ax=axes[1])
axes[1].axvline(x=event_idx, c='pink', linestyle='--', linewidth=0.7)
df['yoy'].plot(ax=axes[2])
axes[2].axvline(x=event_idx, c='pink', linestyle='--', linewidth=0.7)
df['yoy'].diff().plot(ax=axes[3])
axes[3].axvline(x=event_idx, c='pink', linestyle='--', linewidth=0.7)
plt.tight_layout()
plt.show()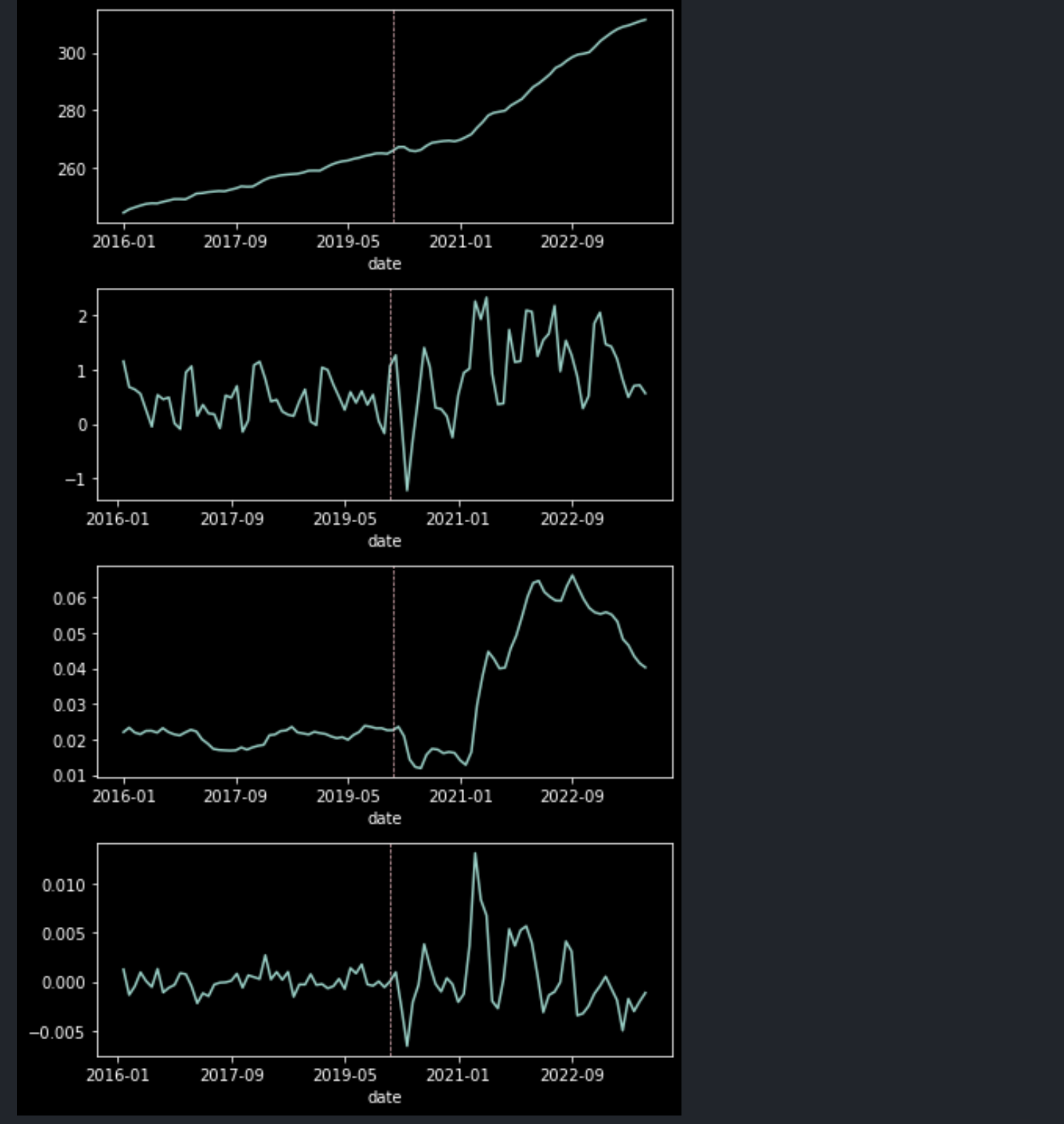
상단부터 순서대로 value, value의 변화율, yoy, yoy의 변화율이다. 가운데 수직선이 코로나가 본격적으로 확산하기 시작한 2020년 1월에 해당한다. 연준이 유동성을 공급하기 시작한 시점과 맞닿기 때문에 첫 번째 데이터(value)에서 수직선 우측 그래프의 경사도가 높아지는 것을 확인할 수 있다.
두 번째 데이터(value.diff())의 우측은 0보다 상단에 위치하여 물가가 떨어지지 않고 계속 오르는 모양새를 보여주며, 그 아래 yoy는 전년 대비 물가가 크게 올랐고, 오른 상태가 유지되는 모습을 보여준다. 마지막 yoy.diff() 전년 동월 대비 물가 증감의 변동률이 코로나 이후 급격히 확대된 것을 보여준다.
이렇게 정성적으로 살펴볼 수 있으나 통계적으로 과연 그 차이가 유의한가?를 확인할 때는 paired t-test를 수행한다. python에서는 scipy 패키지로 간단히 수행할 수 있다. paired t-test의 경우 두 비교 대상의 데이터 길이가 같아야 함에 유의한다.
from scipy import stats
print(stats.ttest_rel(df['value'].diff().dropna().loc['2019-01':'2019-12'],
df['value'].diff().dropna().loc['2021-01':'2021-12']))
print(stats.ttest_rel(df['yoy'].loc['2019-01':'2019-12'],
df['yoy'].loc['2021-01':'2021-12']))
print(stats.ttest_rel(df['yoy'].diff().dropna().loc['2019-01':'2019-12'],
df['yoy'].diff().dropna().loc['2021-01':'2021-12']))Ttest_relResult(statistic=-3.0930454921018695, pvalue=0.010230311851951779)
Ttest_relResult(statistic=-3.542850119128582, pvalue=0.004609581345573239)
Ttest_relResult(statistic=-2.108403107832839, pvalue=0.05873916489588582)paired의 귀무가설은 "이벤트 전, 후 기간의 평균 차이가 통계적으로 유의하지 않다"다. 평균 검정이므로 선형적인 상승 추세가 존재하는 value를 제외한 나머지 3개 데이터 유형을 확인했고, 그 결과 5% 기각역에 진입한 value.diff()와 yoy는 귀무가설을 기각하고 두 기간의 평균 차이가 유의함을 확인했다.
3. 시계열 정상성 검정
과거의 Core CPI로 다음 달 Core CPI를 예측하는 것이 목표다. 따라서 과거의 데이터 분포가 일정하여 그 분포를 예측에 활용할 수 있다는 가정이 필요하며, 만약 그 가정이 틀렸다면 성립할 수 있도록 데이터를 '정상화'해야 한다.
실무적으로 '정상 시계열'이라 함은 평균과 표준편차가 과거부터 꾸준히 일정함을 의미한다. 분포가 일정하지 않다면 통계 기반 예측을 수행할 수 없다. 시계열의 가장 대표적인 특징 2가지는 '자기상관성'과 '평균회귀'다. 평균회귀는 예측에 유용하고 자기상관성은 예측을 방해한다. 자기상관성은 과거의 x가 미래의 x에 영향을 미치는 성질을 말하며 이 정도가 강하면 시간이 지남에 따라 분포가 계속해서 달라지기 때문이다.
따라서 이러한 자기상관성을 제거하기 위해 앞서 우리가 사용한 것처럼 차분(diff())을 하거나 로그변환을 수행할 수 있다. 그 횟수에는 제약이 없으나 어느 정도의 설명력을 유지하고 정보손실을 최소화하기 위해 2차 차분까지가 실무적으로 적절하다. 2차 차분을 굳이 해석하면 변화량의 차이, 증감 정도가 되겠다.
정상성 검정은 Augmented Dickey-Fuller 방법론(이하 ADF)이 주로 활용된다.
from statsmodels.tsa.stattools import adfuller
def adf_test(data, name):
result = adfuller(data.values)
print(name)
print(f'>> statistics: {result[0]:.3f}')
print(f'>> p_value: {result[1]:.3f}')
print(f'>> critical values(5%):{result[4]["5%"]:.3f}')
if result[1] < 0.05:
print('pass!! :)')
else:
print('fail :(')
print('--------------------------')
adf_test(df['value'], name='value')
adf_test(df['value'].diff().dropna(), name='value (d:1)')
adf_test(df['value'].diff().diff().dropna(), name='value (d:2)')
adf_test(df['yoy'], name='yoy')
adf_test(df['yoy'].diff().dropna(), name='yoy (d:1)')
adf_test(df['yoy'].diff().diff().dropna(), name='yoy (d:2)')value
>> statistics: 2.862
>> p_value: 1.000
>> critical values(5%):-2.894
fail :(
--------------------------
value (d:1)
>> statistics: -1.404
>> p_value: 0.580
>> critical values(5%):-2.898
fail :(
--------------------------
value (d:2)
>> statistics: -3.116
>> p_value: 0.025
>> critical values(5%):-2.899
pass!! :)
--------------------------
yoy
>> statistics: -0.891
>> p_value: 0.791
>> critical values(5%):-2.898
fail :(
--------------------------
yoy (d:1)
>> statistics: -2.107
>> p_value: 0.242
>> critical values(5%):-2.898
fail :(
--------------------------
yoy (d:2)
>> statistics: -2.840
>> p_value: 0.053
>> critical values(5%):-2.898
fail :(
--------------------------정상성을 검정하는 여러 가지 방식이 있는데 ADF는 검증을 위해 '단위근의 존재'를 확인하는 방식이다.
y_t = a*y_t-1 + e_t-1
위와 같은 식에서 a의 해(근)를 찾는 상황이다. 이때 a=1이 될 수 있는가?를 확인한다. 만약 a=1이라면 y_t = y_t-1 + e_t-1이고 모든 시점을 전개했을 때 y_t = e_0 + e_1 + ... + e_t-1이 된다. 즉, y_t는 예측 불가한 오차의 누적 합이므로 예측이 불가하다.
한편 a=0일 때에도 y_t = e_t-1로, 모든 항이 오차가 되는데 이 때는 y_t-1과 y_t가 서로 독립이다. 즉, 자기상관성이 없고 오차 범위 내 일정한 분포(일정한 변동성)를 가지므로 예측이 가능하다.
정상시계열은 a<1이다. 직전 값(y_t-1)에 1보다 작은 가중치를 곱하고 외부 충격(e)을 더하여 자기 자신이 되는데, a<1이라면 먼 과거에 발생한 외부 충격은 현재까지 영향을 주는 비율이 적으므로 시간이 지남에 따라 시계열이 '발산'하지 않을 수 있다. a>=1이라면 시계열은 시간이 지남에 따라 발산하고 각 데이터포인트는 오차의 합이 되어 random이다.
돌아와서, 위에서 수행한 adf 검정 결과 value의 2차 차분 데이터만 단위근이 존재한다는 귀무가설을 기각하고 정상성을 만족함을 확인했다.
한편, 정상성은 자기상관함수를 통해서도 시각적으로 발견할 수 있다.
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
fig, axes = plt.subplots(ncols=2, nrows=4, figsize=(12,10))
plot_acf(df['value'], ax=axes[0,0])
plot_acf(df['value'].diff().dropna(), ax=axes[1,0])
plot_acf(df['yoy'], ax=axes[2,0])
plot_acf(df['yoy'].diff().dropna(), ax=axes[3,0])
plot_pacf(df['value'], ax=axes[0,1])
plot_pacf(df['value'].diff().dropna(), ax=axes[1,1])
plot_pacf(df['yoy'], ax=axes[2,1])
plot_pacf(df['yoy'].diff().dropna(), ax=axes[3,1])
plt.tight_layout()
plt.show()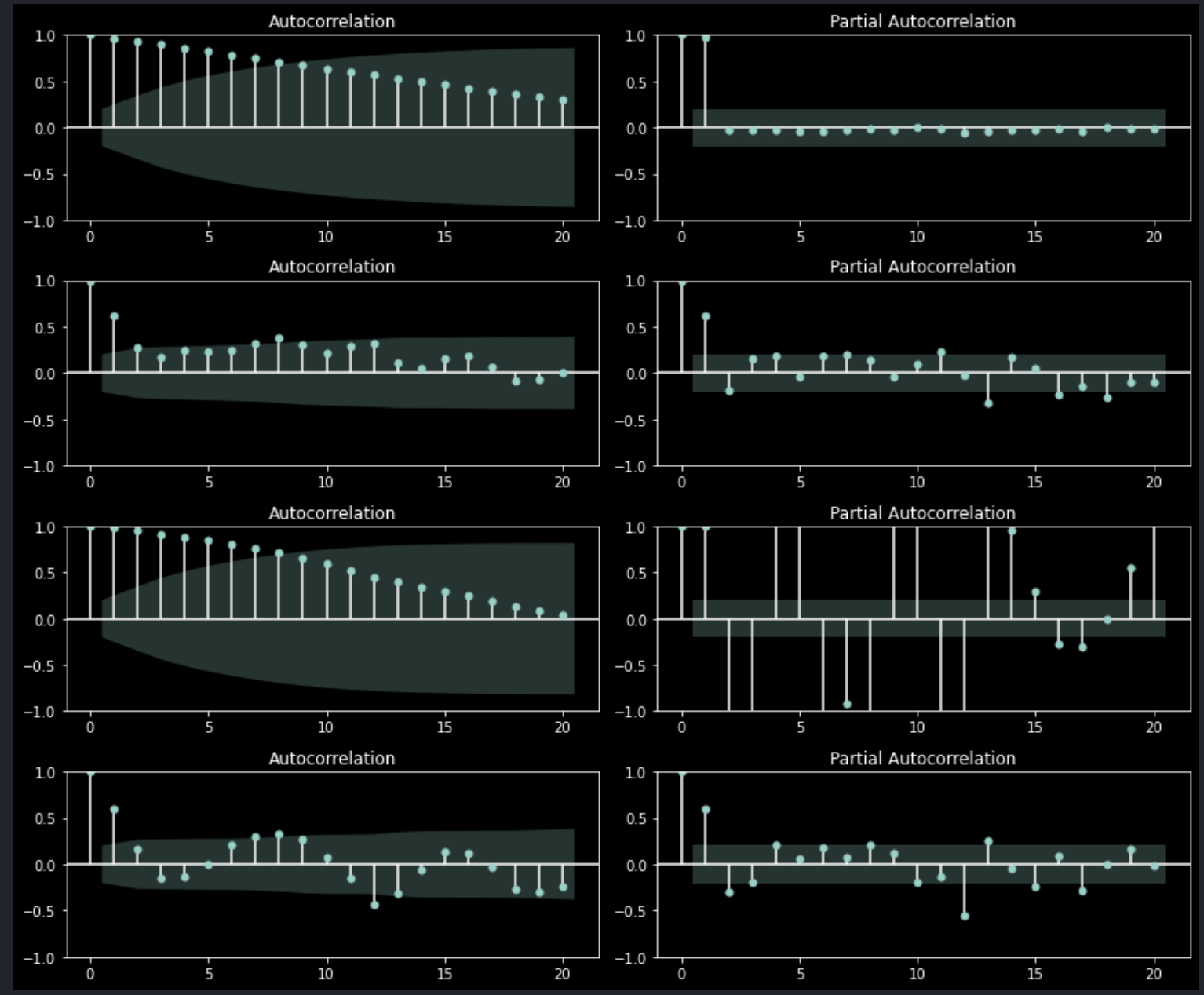
좌측은 자기상관성, 우측은 부분자기상관성을 각 시차별로 보여주며 상단부터 2개는 각각 value와 value의 1차 차분, 하단 2개는 yoy와 yoy의 1차 차분 데이터를 분석한 결과다.
이렇게 1차 차분을 수행하더라도 직전 데이터와의 상관성이 여전히 존재한다. 반면, 아래와 같이 2차 차분을 수행하면 1개 이상의 시차에 대해 모두 상관성이 소거된다.
fig, axes = plt.subplots(ncols=2, nrows=2, figsize=(8,6))
plot_acf(df['value'].diff().diff().dropna(), ax=axes[0,0])
plot_acf(df['yoy'].diff().diff().dropna(), ax=axes[1,0])
plot_pacf(df['value'].diff().diff().dropna(), ax=axes[0,1])
plot_pacf(df['yoy'].diff().diff().dropna(), ax=axes[1,1])
plt.tight_layout()
plt.show()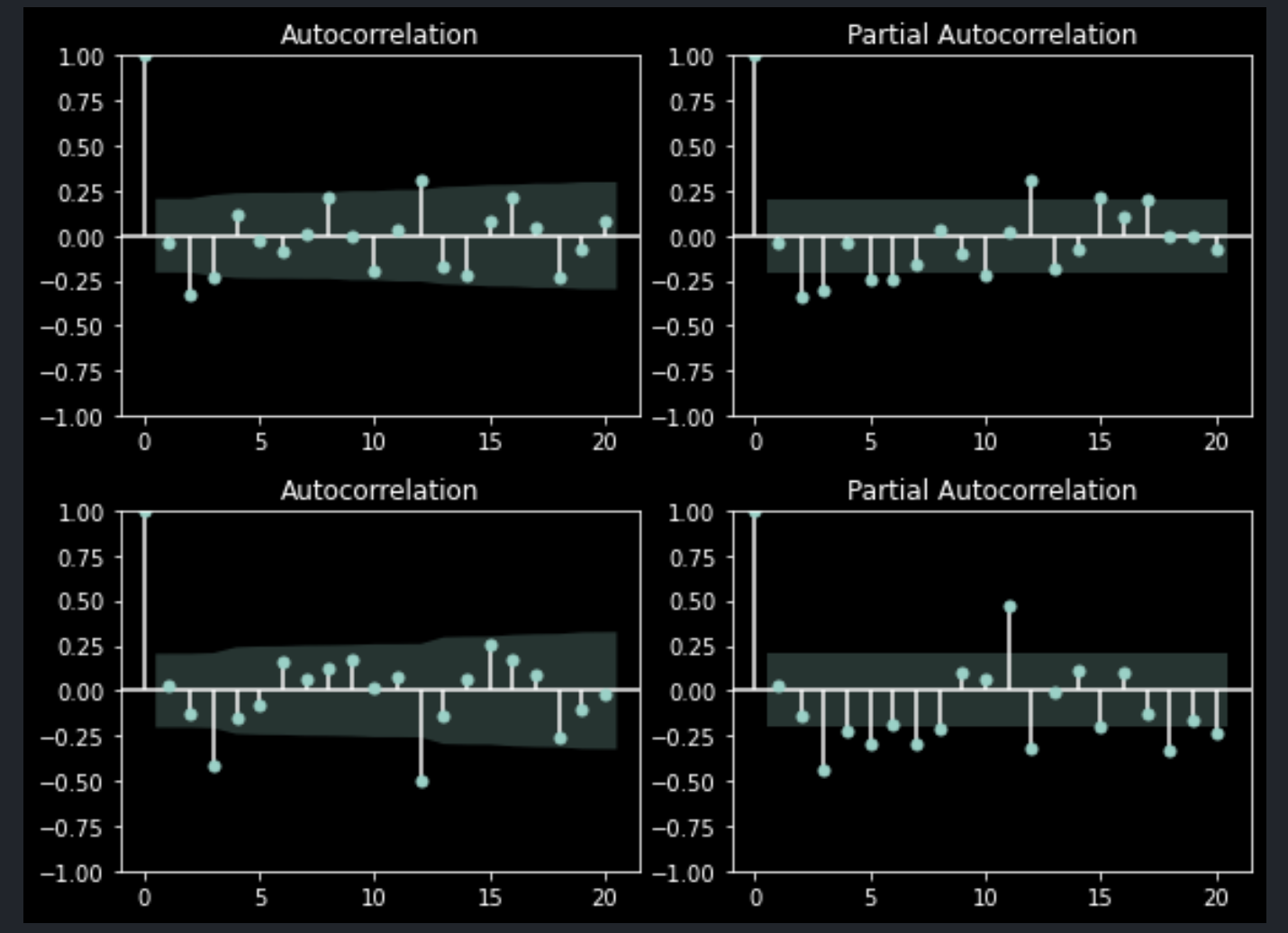
adf 검정 결과처럼 yoy의 2차 차분보다 value의 2차 차분이 기각역 내에 충분히 포함되어 있음을 알 수 있다.
4. ARIMA 모델링
한편, auto_arima 패키지를 통해 자동으로 차분 횟수를 결정할 수 있다. 그뿐만 아니라 ar(p), ma(q) 각 모형의 차수도 함께 결정하여 최적의 arima 계산식을 결정한다. arima는 ar(p), ma(q) 모형을 합친 형태로 차분까지 고려한다. 즉, 시계열의 오차 이동평균과 자기상관성을 모두 계산에 포함하되 d차 차분한 데이터로 계산을 수행한다.
- ar(p): y를 추정하는 데에 지난 p기간의 y(자기 자신)를 고려하겠다
- ma(q): y를 추정하는 데에 지난 q기간의 e(오차)를 고려하겠다
- i(d): ar(p), ma(q) 모델링을 d차 차분한 데이터로 수행한다.
model_value = pm.auto_arima(
y=data_value,
d=1,
start_p=0, max_p=3,
start_q=0, max_q=3,
m=1,
seasonal=False,
stepwise=True,
trace=True
)Performing stepwise search to minimize aic
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=188.093, Time=0.31 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=144.993, Time=0.11 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=150.317, Time=0.10 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=260.225, Time=0.03 sec
ARIMA(2,1,0)(0,0,0)[0] intercept : AIC=143.666, Time=0.07 sec
ARIMA(3,1,0)(0,0,0)[0] intercept : AIC=143.753, Time=0.08 sec
ARIMA(2,1,1)(0,0,0)[0] intercept : AIC=145.047, Time=0.13 sec
ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=143.142, Time=0.07 sec
ARIMA(1,1,2)(0,0,0)[0] intercept : AIC=143.547, Time=0.21 sec
ARIMA(0,1,2)(0,0,0)[0] intercept : AIC=141.235, Time=0.06 sec
ARIMA(0,1,3)(0,0,0)[0] intercept : AIC=143.157, Time=0.07 sec
ARIMA(1,1,3)(0,0,0)[0] intercept : AIC=141.837, Time=0.19 sec
ARIMA(0,1,2)(0,0,0)[0] : AIC=170.584, Time=0.05 sec
Best model: ARIMA(0,1,2)(0,0,0)[0] intercept
Total fit time: 1.500 secondsmodel_yoy = pm.auto_arima(
y=data_yoy,
d=1,
start_p=0, max_p=3,
start_q=0, max_q=3,
m=1,
seasonal=False,
stepwise=True,
trace=True
)Performing stepwise search to minimize aic
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=-715.722, Time=0.05 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=-750.544, Time=0.06 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=-745.228, Time=0.10 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=-717.252, Time=0.04 sec
ARIMA(2,1,0)(0,0,0)[0] intercept : AIC=-755.869, Time=0.12 sec
ARIMA(3,1,0)(0,0,0)[0] intercept : AIC=-757.021, Time=0.15 sec
ARIMA(3,1,1)(0,0,0)[0] intercept : AIC=-756.707, Time=0.09 sec
ARIMA(2,1,1)(0,0,0)[0] intercept : AIC=-746.786, Time=0.15 sec
ARIMA(3,1,0)(0,0,0)[0] : AIC=-758.600, Time=0.04 sec
ARIMA(2,1,0)(0,0,0)[0] : AIC=-757.636, Time=0.05 sec
ARIMA(3,1,1)(0,0,0)[0] : AIC=-758.310, Time=0.07 sec
ARIMA(2,1,1)(0,0,0)[0] : AIC=-749.194, Time=0.06 sec
Best model: ARIMA(3,1,0)(0,0,0)[0]
Total fit time: 0.984 secondsvalue 데이터로는 1차 차분 데이터에 대해서 MA(2)로 최적의 모델링이 가능하다. 다시 말해 정상성을 확보하는 2차 차분이 아닌 1차 차분까지만 수행하고 지난 2개의 error term으로 y를 예측하겠다는 의미다.
auto_arima로 적합시킨 모형의 요약통계를 아래와 같이 확인할 수 있다.
print(model_value.summary()) SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 94
Model: SARIMAX(0, 1, 2) Log Likelihood -66.618
Date: Tue, 05 Dec 2023 AIC 141.235
Time: 00:36:30 BIC 151.365
Sample: 01-01-2016 HQIC 145.325
- 10-01-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.7222 0.126 5.725 0.000 0.475 0.969
ma.L1 0.7906 0.116 6.837 0.000 0.564 1.017
ma.L2 0.3484 0.097 3.576 0.000 0.157 0.539
sigma2 0.2435 0.036 6.741 0.000 0.173 0.314
===================================================================================
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 7.88
Prob(Q): 0.94 Prob(JB): 0.02
Heteroskedasticity (H): 2.60 Skew: 0.66
Prob(H) (two-sided): 0.01 Kurtosis: 3.54
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).print(model_yoy.summary()) SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 94
Model: SARIMAX(3, 1, 0) Log Likelihood 444.380
Date: Tue, 05 Dec 2023 AIC -880.760
Time: 00:37:19 BIC -870.630
Sample: 01-01-2016 HQIC -876.670
- 10-01-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.7229 0.129 5.585 0.000 0.469 0.977
ar.L2 -0.1489 0.123 -1.210 0.226 -0.390 0.092
ar.L3 -0.1835 0.084 -2.181 0.029 -0.348 -0.019
sigma2 4.104e-06 5.46e-07 7.514 0.000 3.03e-06 5.17e-06
===================================================================================
Ljung-Box (L1) (Q): 0.05 Jarque-Bera (JB): 118.85
Prob(Q): 0.83 Prob(JB): 0.00
Heteroskedasticity (H): 5.96 Skew: 1.10
Prob(H) (two-sided): 0.00 Kurtosis: 8.08
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).Ljung-Box는 잔차의 정상성을 검정한다. 앞서 확인한 정상성은 모델이 적합할 대상에 대한 정상성이다. 즉, 데이터가 발산하거나 랜덤 워크가 아니라 특정 분포를 유지하는가?를 검정한 것이며, Ljung-Box가 검정하는 것은 모델이 적합하고 남은 오차끼리 서로 자기상관성이 없는가? 에 대한 내용이다.
Ljung-Box의 귀무가설은 잔차 자기상관성이 0이다(존재하지 않는다)이며, 위 두 케이스에서 모두 Prob(Q)가 0.05보다 크므로 모델이 잔차에 정상성을 남기지 않고 잘 적합시켰다고 볼 수 있다.
Heteroskedasticity는 이분산성, 그러니까 '시간 경과에 따라 분산이 달라짐'을 의미한다. 이분산성이 존재한다면 전 시차에 걸쳐 잔차가 일정 분포를 유지하지 못하는 것이며, 온전히 잔차만 걸러진 것이라 확신할 수 없다. 따라서 이분산성이 아닌 동분산성에 대한 잔차 가정을 만족하는가를 검증해야 한다.
한편, Jarque-Bera 검정은 잔차의 정규성을 확인한다. 이분산성 검정의 귀무가설은 '잔차의 분산이 일정하다'이며, Jarque-Bera 검정 귀무가설은 '잔차가 정규성을 만족한다'이다. 두 검정에서 P-value는 0.05보다 작으므로 기각한다.
동분산성과 정규성을 만족시키는 여러 방법론이 존재한다. 하지만 단일 시계열로 미래값을 예측하는 것은 외생변수의 존재를 고려하지 못하므로 근본적인 제약이 있다. 따라서 이와 같은 단일 시계열에 대해 동분산성과 정규성을 만족시키더라도 예측의 한계가 뚜렷하기에 그 제약을 인정하고 부가적인 처리 없이 예측을 수행한다.
(*auto_arima로 적합한 모형 인스턴스는 잔차 검정 결과에 대해 아래와 같이 시각화 함수를 함께 제공한다.)
model_value.plot_diagnostics(figsize=(8,6))
plt.tight_layout()
plt.show()
model_yoy.plot_diagnostics(figsize=(8,6))
plt.tight_layout()
plt.show()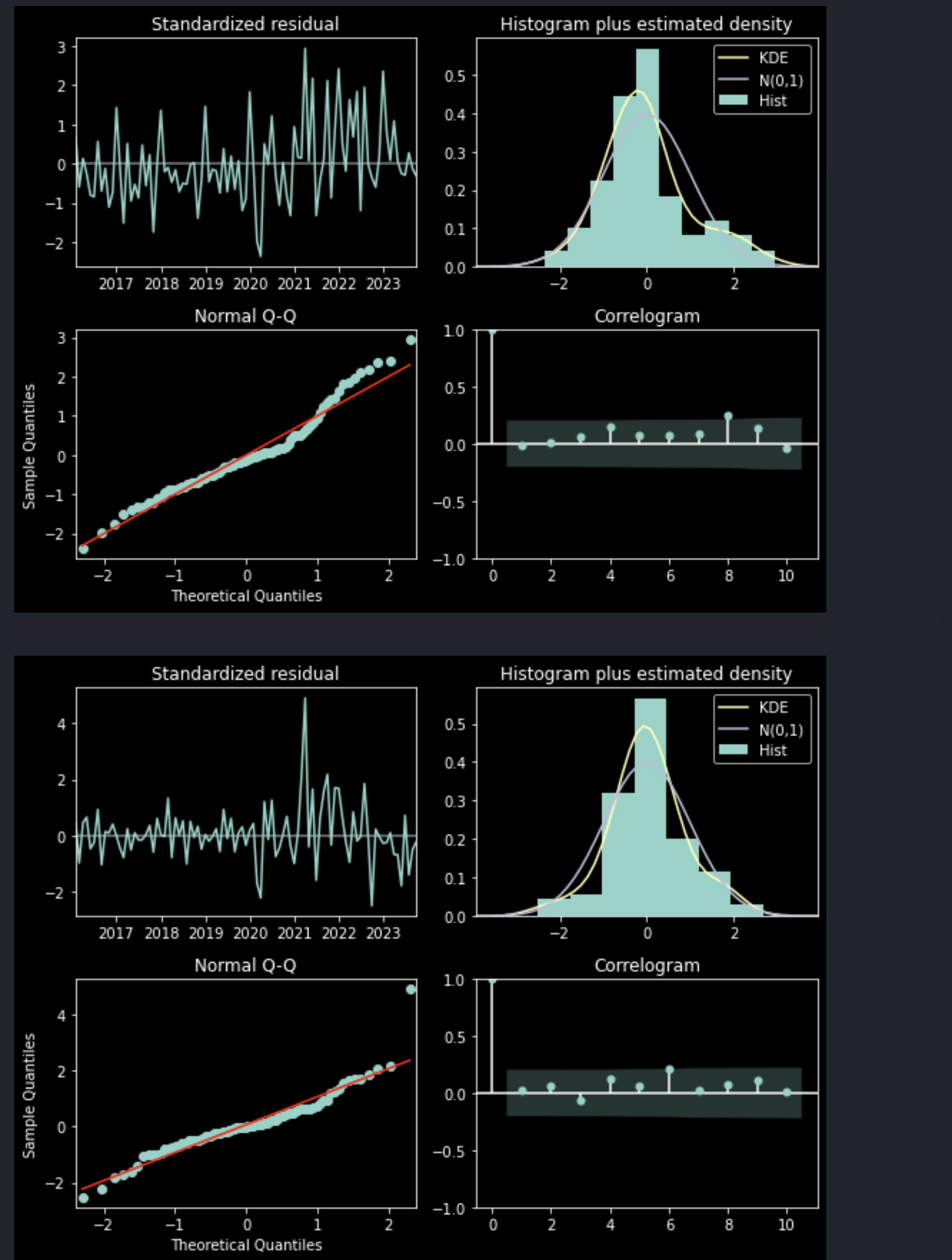
5. ARIMA 예측 결과 시각화
value(원본 데이터), yoy(전년 동월 대비 증감) 각각 적합시킨 ARIMA 모형을 통해 다음 달의 yoy를 예측한다. 주의할 점은 value에 적합시킨 모형의 예측값은 value의 분포로, yoy에 적합시킨 예측값은 yoy의 분포로 그 결과를 추정하기 때문에 value의 경우 yoy의 형태로 변환해야 한다.
- 예시) value 기존 값(2016-01~2023-10)과 예측 값(2023-11-01~2024-03-01)
date
2016-01 244.528
2016-02 245.680
2016-03 246.358
2016-04 246.992
2016-05 247.544
...
2023-06 308.910
2023-07 309.402
2023-08 310.103
2023-09 310.817
2023-10 311.380
Name: value, Length: 94, dtype: float642023-11-01 311.956943
2023-12-01 312.625214
2024-01-01 313.347425
2024-02-01 314.069637
2024-03-01 314.791848
Freq: MS, dtype: float64- 예시) yoy 기존 값(2016-01~2023-10)과 예측 값(2023-11-01~2024-03-01)
date
2016-01 NaN
2016-02 NaN
2016-03 NaN
2016-04 NaN
2016-05 NaN
...
2023-06 0.048290
2023-07 0.046529
2023-08 0.043492
2023-09 0.041465
2023-10 0.040309
Name: yoy, Length: 94, dtype: float642023-11-01 0.040332
2023-12-01 0.040893
2024-01-01 0.041507
2024-02-01 0.041863
2024-03-01 0.041926
Freq: MS, dtype: float64
value에서 yoy로의 변환은 간단히 pct_change(period=12) 함수만 적용해 주면 된다. 예측 결과를 비교하면 아래와 같다.
data_value_pred = model_value.predict(n_periods=5)
data_value_all = pd.Series(list(data_value.values) + list(data_value_pred.values)).pct_change(periods=12).dropna().reset_index(drop=True)
data_value_all.plot()
plt.axvline(x=len(data_value_all)-len(data_value_pred), c='pink', linewidth=0.7, linestyle='--')
plt.show()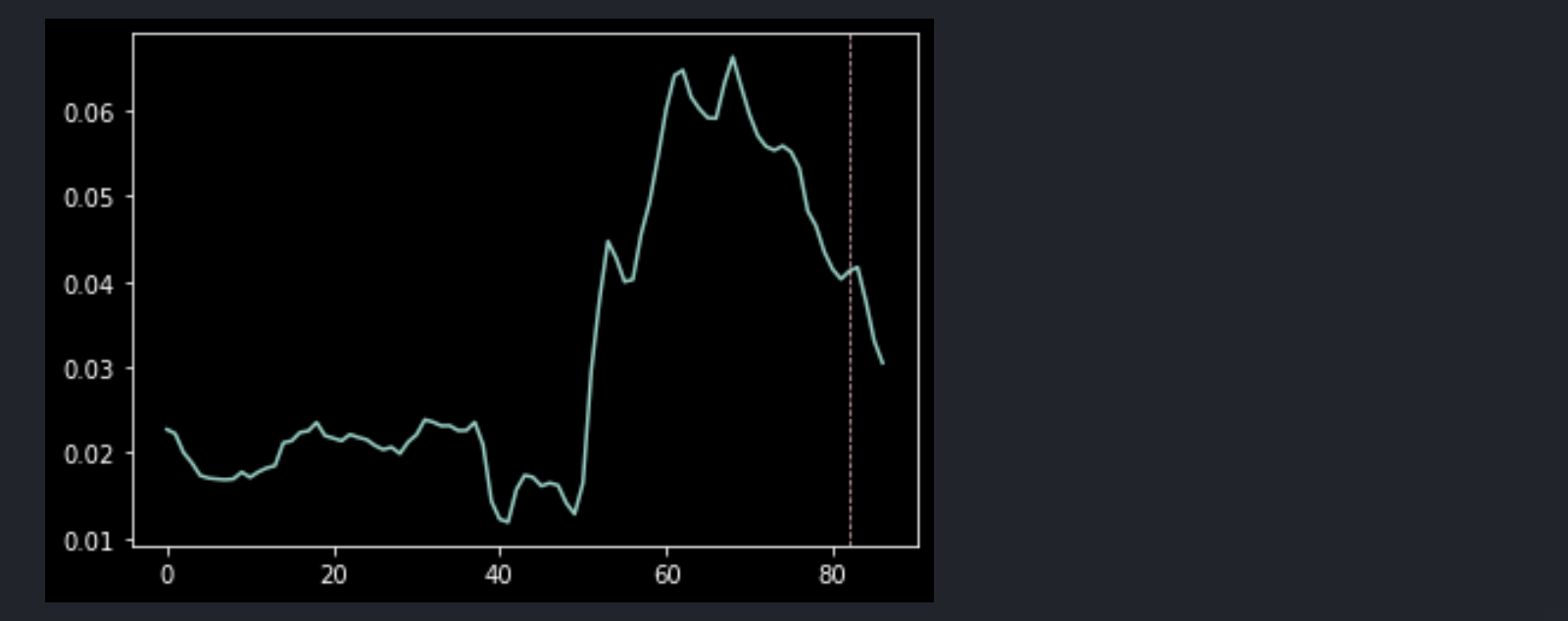
data_yoy_pred = model_yoy.predict(n_periods=5)
data_yoy_all = pd.Series(list(data_yoy.values) + list(data_yoy_pred.values)).dropna().reset_index(drop=True)
data_yoy_all.plot()
plt.axvline(x=len(data_yoy_all)-len(data_yoy_pred), c='pink', linewidth=0.7, linestyle='--')
plt.show()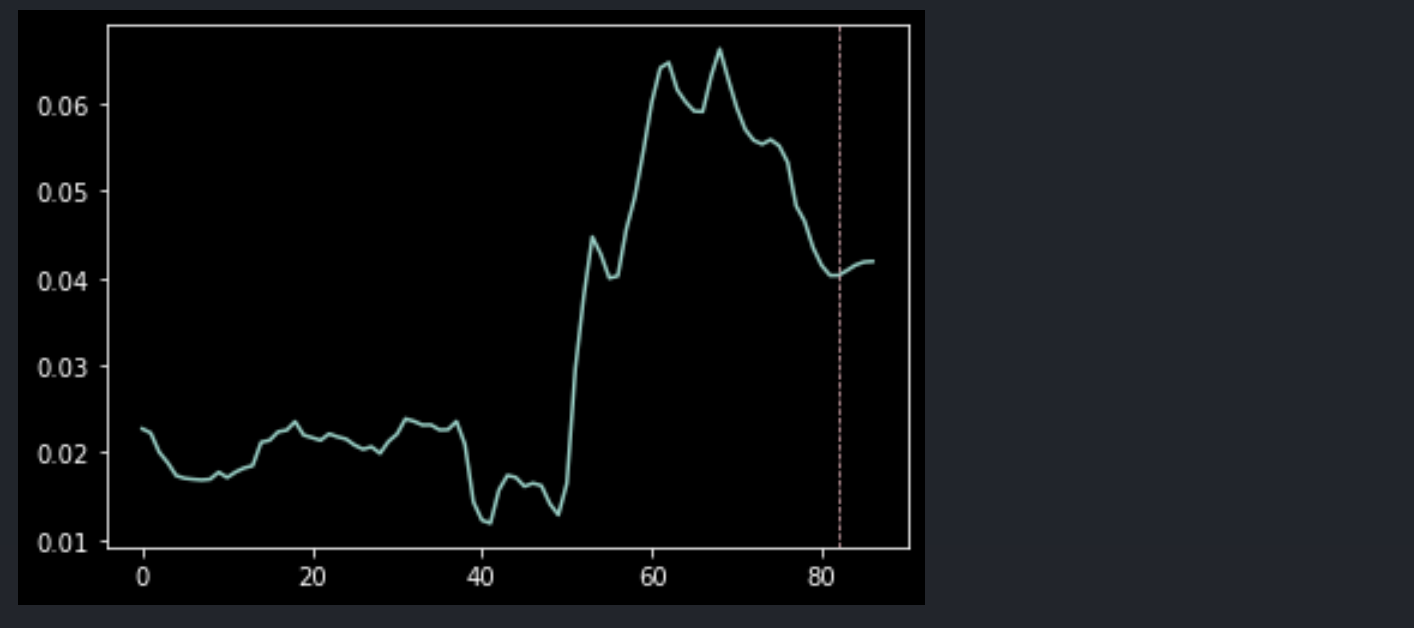
이렇게 같은 데이터에 기반한 같은 모형이라도 집계 방식에 따라 전혀 다른 방향의 예측을 수행할 수 있다. 이 부분이 단변량 시계열의 제약이며, 경제 요인과 같은 연쇄적이고 복잡한 데이터에 취약하다.
따라서 2개 이상의 독립변수를 고려할 수 있는 VaR 같은 다변량 모형을 다룰 수 있어야 하며, 특히 기본적인 회귀모형과 인과추론 방법론을 통해 변수를 찾고 설명력을 높이는 것도 반드시 필요하겠다.