본 시리즈는 파이썬으로 시계열 자기상관 특성 및 마켓, 안전자산, 대체자산 등과의 동시간대 연관성을 분석하고 Apple Inc(AAPL) 주가를 예측한다.
튜토리얼 작성을 위해 금융전략을 위한 머신러닝(한빛미디어), 실전 시계열 분석(한빛미디어) 외 야후파이낸스 및 FRED API 공식문서 등을 참고하였으며 작업 과정에서 추가로 참고하게 되는 자료들은 이후 각 편 내에 서술하도록 하겠다.
1편에서는 간단히 데이터를 불러와 누락된 분포를 살피고, 시계열 기간을 동일하게 맞춘다. 그 다음, 예측에 필요한 데이터를 추출하기 위한 시계열 분석 작업을 간단히 수행하도록 한다.
Step 1. Import Packages

numpy와 pandas를 포함해 seaborn, matplotlib은 데이터 분석을 위해 언제나 기본적으로 설치해둔다. 관련하여 기타 세팅은 자유롭게 설정하면 되는데, '# MacOS - 한글폰트' 부분은 맥 사용자가 Matplotlib 차트를 그렸을 때 한글이 깨지는 현상을 방지하는 부분이니 참고 바란다.

예측 분석을 수행할 모델을 선택하기 위해서는 모델링 과정에서 여러 모델을 비교 분석하게 된다. 우리는 회귀 예측을 목표로 하며 이를 위해 선형 모델, 트리 기반 모델, 거리 기반 모델 및 앙상블 모델을 기본적으로 사용할 예정이다. 또 scikit-learn에서 제공하는 신경망 모형도 함께 불러왔으며 이는 이후 신경망에 '기억'의 개념을 포함하는 LSTM 모델과 비교하기 위함이다. LSTM은 다분히 시계열스러운 분석기법이므로 대표적인 시계열 모델 ARIMA와 함께 구현해 볼 것이다. 추후 PyTorch 혹은 Keras를 사용해 LSTM을 구현할 것인데, 자주 사용하는 패키지가 있다면 미리 불러와도 좋다.
Step 2. Load Datasets

tickers_i는 동종 산업 내 연관자산의 티커명(좌측부터 애플, 테슬라, 마이크로소프트, 메타, 아마존), tickers_m은 시장 내 연관 인덱스 티커명(주석으로 표기)이다. 우리는 시계열 예측을 위해 애플 주가의 과거 데이터(자기상관성 활용)뿐만 아니라 동시간 대의 연관 자산 및 시장 움직임을 모두 포함한 횡/종단면 데이터를 통합 활용할 것이다.
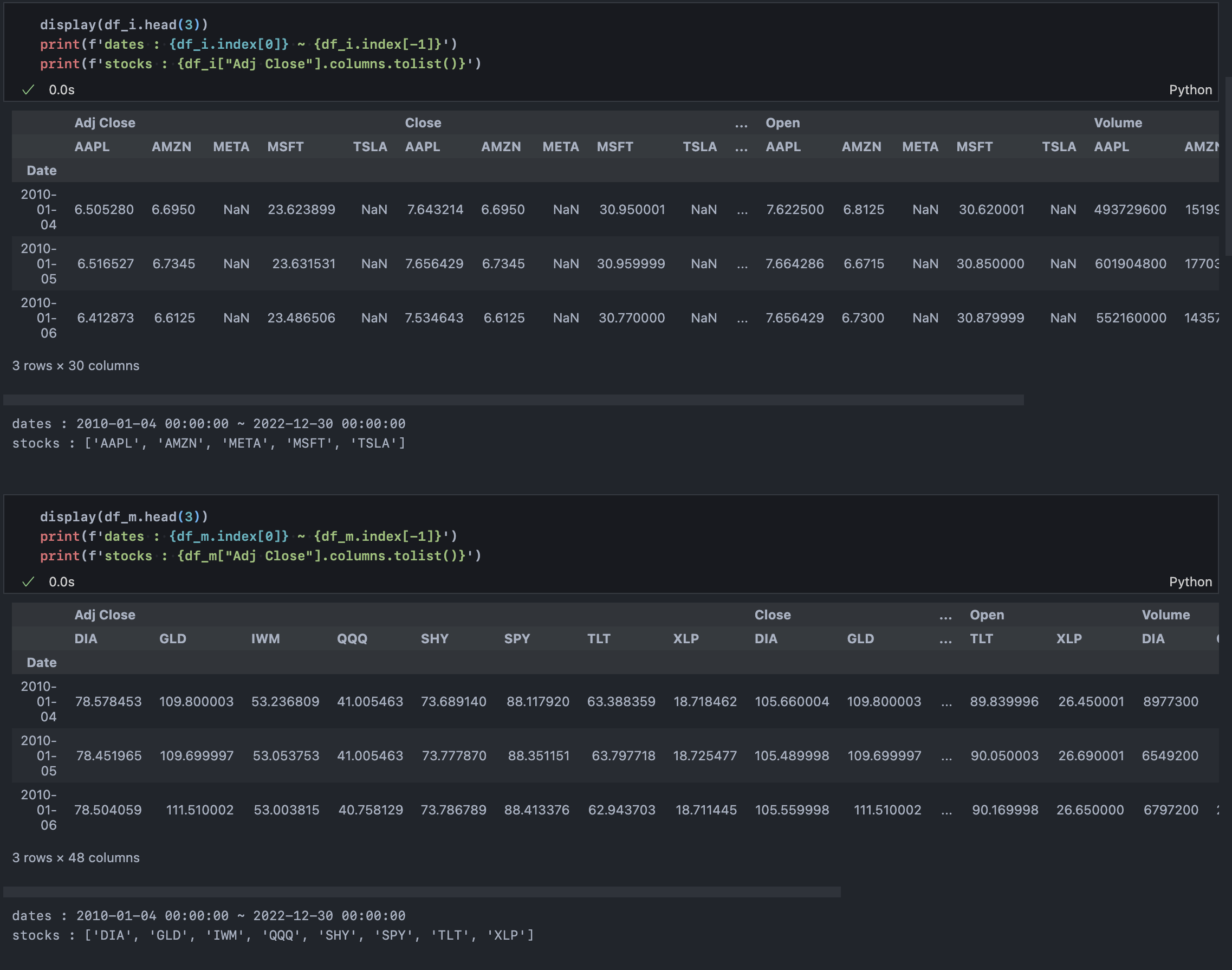
데이터를 살피면 의도대로 2010년 1월 4일부터 2022년 12월 30일까지 데이터가 동일하게 불러졌으나 META와 TSLA의 경우 앞쪽 값이 누락된 것을 확인할 수 있다. 이와 같이 상장일이 차이 나거나 데이터 공급사의 집계 문제로 각 자산별 시계열이 일치하지 않을 수 있는데, 그렇다면 해당 자산을 제외하거나 전체 자산을 해당 자산에 맞게 시계열을 일치시켜줘야 한다. 그 기준을 잡기 위해서는 누락 값의 분포를 확인할 필요가 있겠다.
Step 3. Drop NA's

자산 그룹(df_i)의 수정종가(Adj Close) 데이터로 누락값을 확인해보자. META의 경우 약 18%, TSLA는 약 4%가 부족하다. 앞에서 우리는 2010년부터의 주가정보를 불러왔으나 사실 주가 예측에 10년 전 데이터를 사용하는 경우는 많지 않다. 시장 국면이 빠르게 달라지기 때문이다. 따라서 미리 충분한 데이터를 불러온 만큼 META의 기준에 맞게 18%가량의 과거 데이터를 제거해주자.
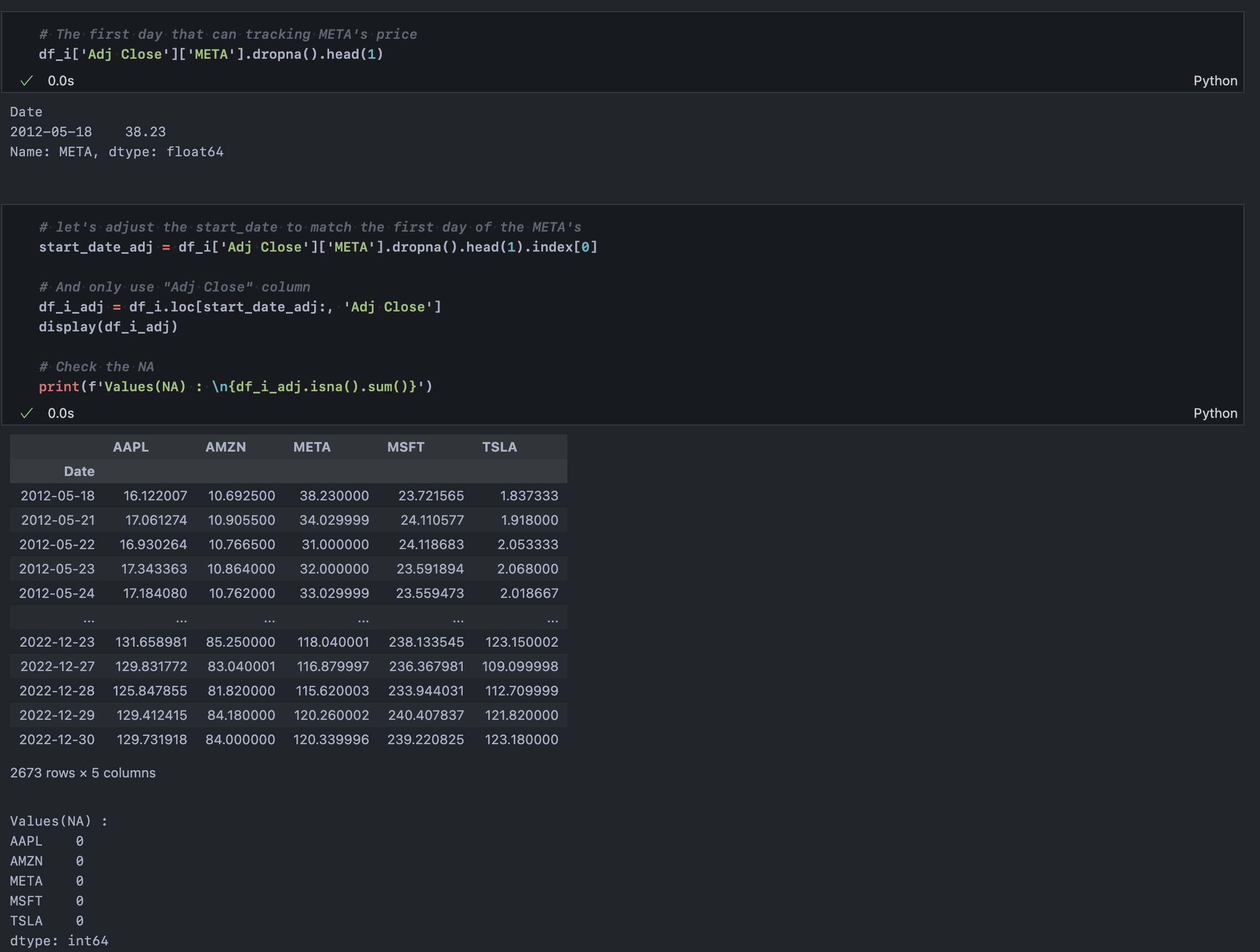
META의 수정종가 기준 데이터가 발생한 첫 날짜는 2012년 5월 18일이다. 해당 날짜 인덱스를 기점으로 전체 데이터를 조정해주었다.
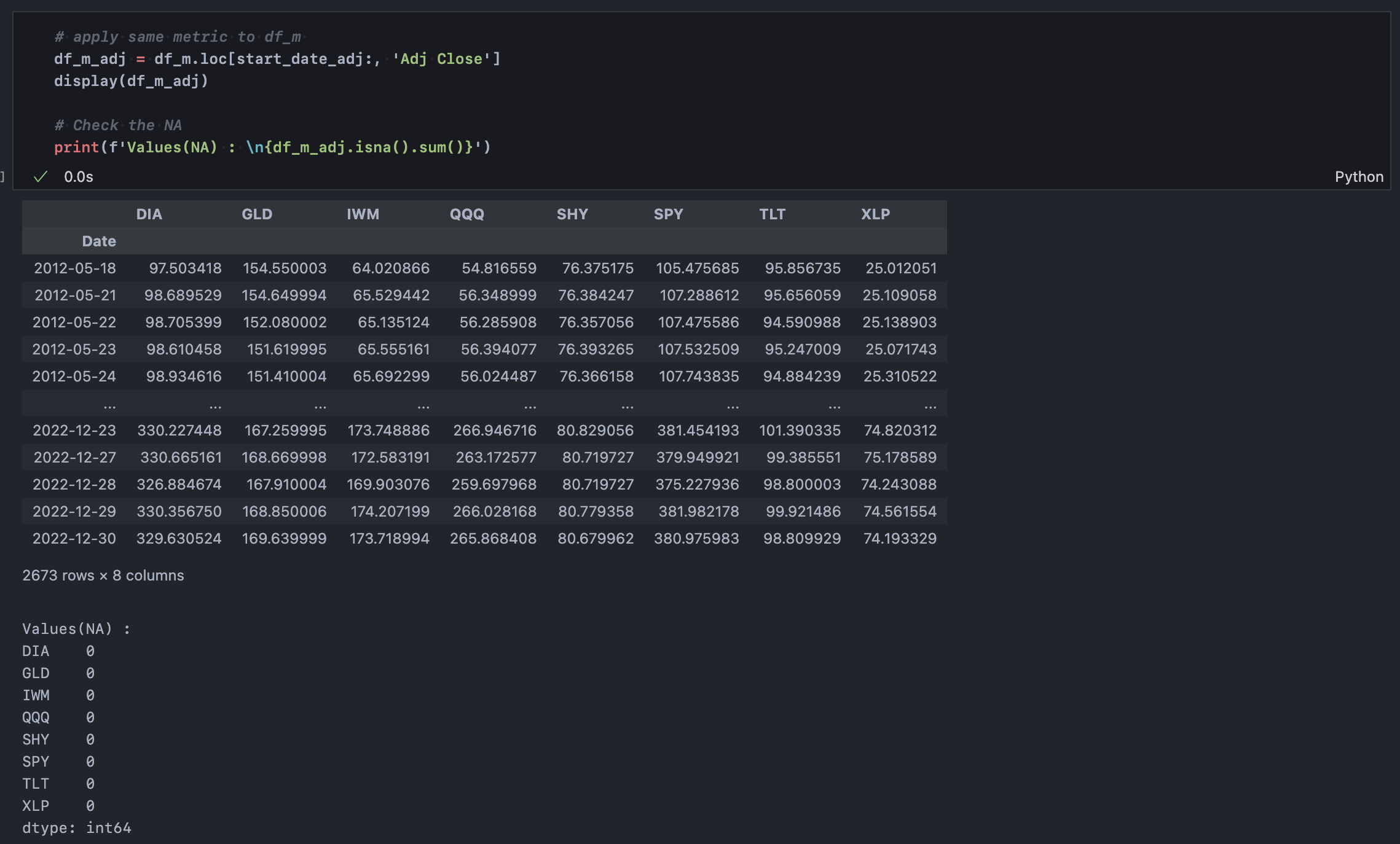
마찬가지로 시장 인덱스(df_m)도 동일하게 시계열을 조정해주면 된다.
Step 4. 예측 안정성 확보
본 편의 핵심이자 가장 중요한 부분이다. 시계열 분석이 정상적으로 수행되기 위해서는 데이터셋이 안정적이어야 한다. 즉, 시간에 따라 분포(평균, 분산)가 달라지지 않아야 하는데 이는 시계열 데이터만의 특수성이자 분석을 위한 기본 가정이다.
예를 들어보자. 만약 이번 주의 통계적 분포와 다음 주의 통계적 분포가 전혀 다르다면 이번 주의 분포를 통해 학습한 예측 모델이 다음 주의 예측에 정상적인 결과를 내놓을 리 없을 것이다. 그런데 주가 데이터의 경우 이러한 성향이 매우 짙다. 소위 주식시장은 우상향 한다고 하지 않는가? 이제 막 상장된 기술 기업은 상장 전 고평가 받은 것을 상장 이후 1~2년 이내 다 뱉어내는 패턴도 존재하고, J커브 같은 스타트업계 용어도 주식시장에서 매우 그럴싸하게 통용된다.
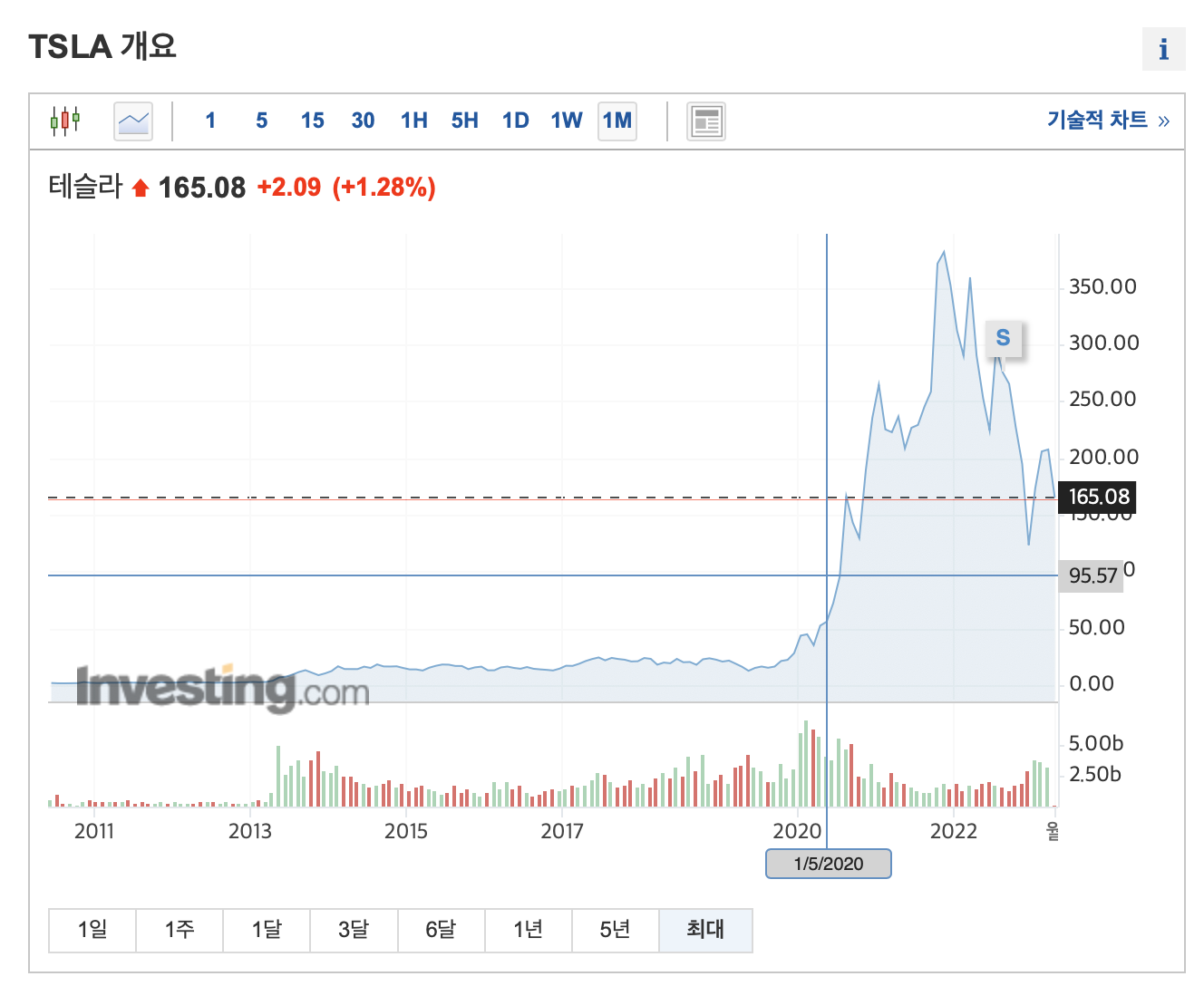
이렇게 테슬라의 경우 2020년 이전과 이후는 전혀 다른 움직임을 보인다. 즉, 통계적 분포와 그 분포에 영향을 미치는 각종 내/외생 변수의 분포까지 달라졌을 것이며, 이는 코로나라는 시장충격이 국면을 완전히 바꿔버린 사례다.
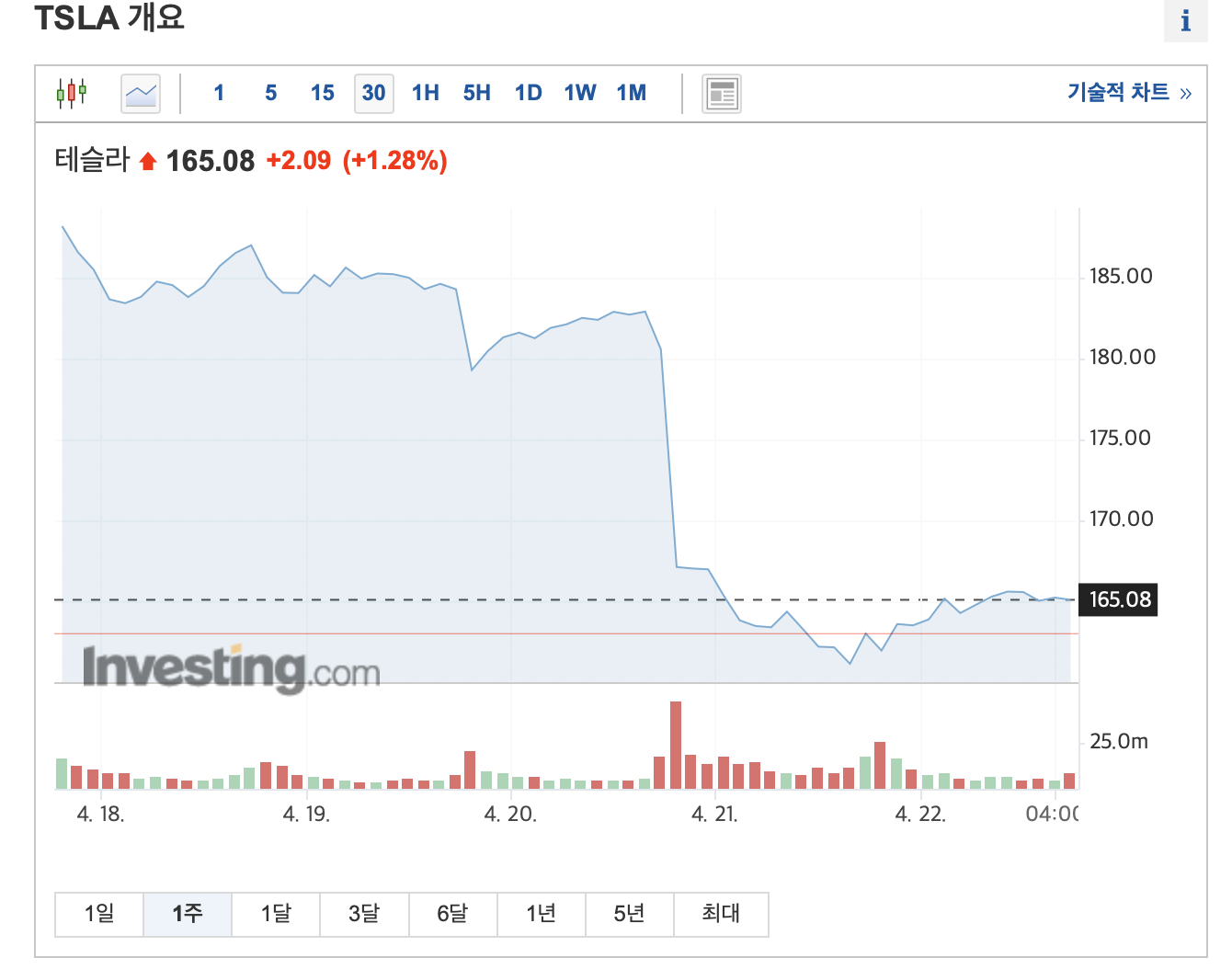
이번에는 더 미시적으로 살펴보자. 이번 한 주(4.17 ~ 4.22) 간 테슬라 주가 움직임은 어떤가? 이전 3일(4.18~4.20)의 주가와 이후 2일(4.21~4.22)의 주가가 같은 분포를 띈다고 할 수 있을까? 그렇다면 이전 3일(4.18~4.20)의 주가로 모델링한 예측 모델이 향후 2일(4.21~4.22)의 주가를 제대로 예측할 수 있을까? 절대 그렇지 않다. 모델은 말 그대로 데이터를 학습하고, 본 것만 기억한다. 즉, 패턴이 달라지면 모델도 달라져야 한다.
그렇기 때문에 데이터의 안정성을 먼저 확보하는 것이 필요하다. 전 시계열에 걸쳐 분포를 동일하게 맞춰 과거에 만든 모델이 앞으로도 (일정 기간 동안) 사용될 수 있어야 하는 것이다.
4-1. 기본 수익률 분포(1일 변화량)
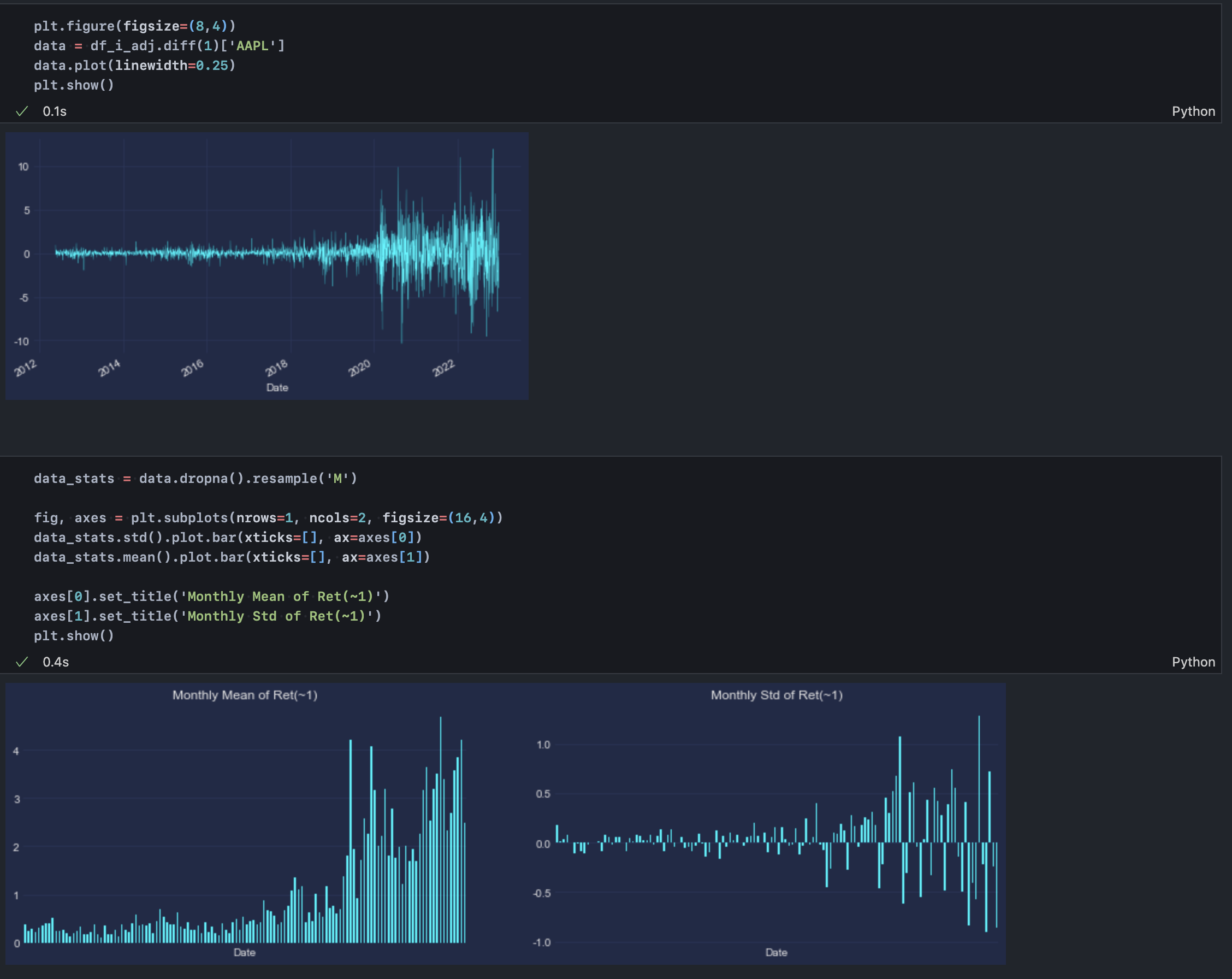
위 첫 번째 차트는 주가의 일간 변화량(어제 대비 오늘의 주가)을 보여준다. 기본적으로 주가에는 복리 효과가 내재되어 있다. 즉 지수적인 상승이 발생하는데, 이에 따라 단순히 어제와 오늘의 주가 차이를 늘어뜨려놓으면 점점 그 진폭이 커진다. 예를 들어 주가가 20달러일 때와 200달러일 때 1% 변화량은 각각 0.2달러, 2달러로 10배가 차이 난다. 특히 애플의 경우에 정석적으로 주가가 우상향 한 케이스이므로 이런 효과가 여실히 드러나는 것이다. 그래서 파이썬을 사용한다면 pct_change를 통해 단순 변화량이 아닌 상대적 비율로써 변화량(%)을 확보할 수 있으나 편의상 log 처리하는 것이 일반적이다. log 처리를 한다는 것의 기술적 맥락은 주가 데이터 분석을 위한 로그 변환의 의미를 참고하길 바란다.
따라서 이러한 데이터를 그대로 사용하긴 어렵다. 두 번째, 세 번째 차트를 보면 각각 월간 평균 및 표준편차 값의 움직임을 확인할 수 있는데, 시간에 따라 이 분포 특성이 크게 달라진다.
4-2. 로그 수익률 1차 차분 분포(로그 변환 + 1일 변화량)
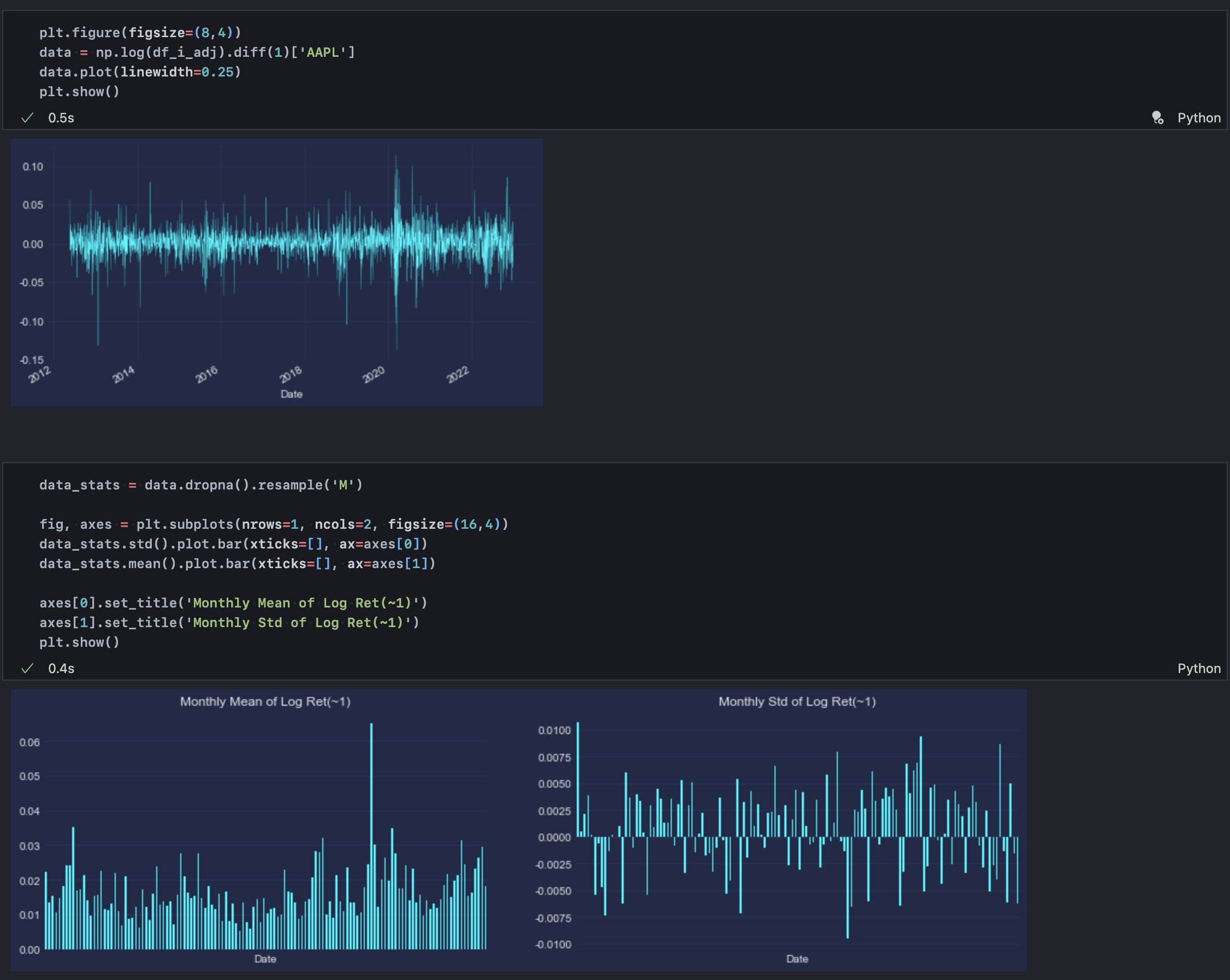
다음은 로그 변환한 가격 변화량(수익률)의 분포다. 앞서 언급한 것처럼 로그 변환 시 각 시점의 상대적 변화량(%)과 거의 유사한 값을 확보할 수 있으며, 분포 통계가 어느 정도 일정해진 것을 확인할 수 있다.
4-3. 로그 수익률 5차 차분 분포(로그 변환 + 5일 변화량)
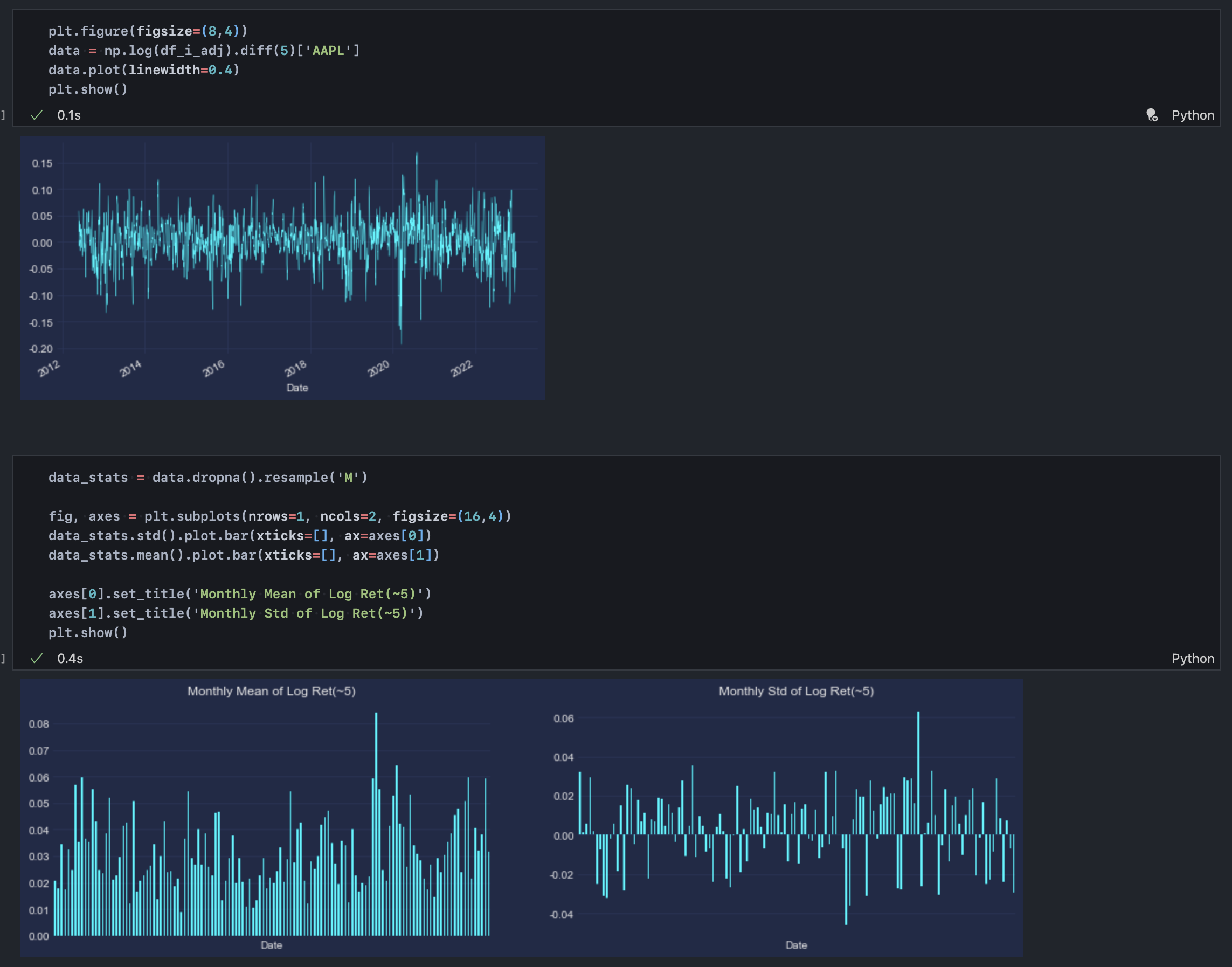
여기서 조금 더 욕심을 낸다면 위와 같이 차분 수를 늘려 분포를 더 안정적으로 만들 수 있다. 차분 횟수는 자기상관성을 제거하기 위한 시계열상 최소 거리와 관련된다. 그렇다고 차분 횟수를 데이터 특성과 무관하게 계속해서 높이면 자연히 정보손실이 발생한다. 내일 주가가 얼마나 변화할지 예측하기 위해 오늘의 주가, 지난주 주가, 지난달 주가 변화량을 살피는 것을 생각해 보자. 뒤로 갈수록 점점 그 관련성이 떨어진다는 것을 쉽게 짐작할 수 있다. 다만, 주가의 경우 요일 특성이 존재하고 매주 금요일의 주가, 그리고 매주 월요일의 주가 변화량은 어느 정도 유사한 분포를 띌 것이다.
이러한 것들을 감으로 판단하기보다 ADF Test(단위근 검정)나 자기상관성 검정 등을 통해 실시하면 좋다. 따라서 본 편에 더해 인사이트를 얻고자 한다면 앞서 확인한 3가지 분포에 대해 정상성을 통계적으로 확인해보길 바란다. 우리는 앞서 미리 statsmodels에서 제공하는 adfuller 패키지를 불러왔다. 해당 패키지를 활용해 단위근 검정을 실시하고 각각의 분포가 정상성을 확보하는지 확인해보자.
참고로 단위근 검정 결과를 해석하기 위해서는 약정상성, 강정상성에 대해 미리 알아둘 필요가 있는데, ADF Test는 약정상성을 만족하는가에 대한 검정 결과를 보여준다. 주의할 점은 강정상성이 약정상성을 반드시 포함하지도 않고, 약정상성이라 해서 그 정도가 약하다는 의미도 아니다. 다만, "데이터가 약정상성을 확보했다면, 최소한 모델이 그 분포를 학습하고 이해하기에 적절하다." 정도로 그 의미를 이해하도록 하자.