Step 1. 토픽모델링이란
토픽모델링은 특정 문서의 확률적 카테고리를 나누는 비지도학습 방법론이며 기본적인 컨셉은 다음과 같다.
- 문서는 단어의 조합이다.
- 문서 내 함께 등장하는 단어는 서로 연관성이 있다.
- 모든 문서에서 자주 등장하는 단어는 특수한 의미를 내포하지 않는다.
- 반면, 그렇지 않은 단어는 특수한 의미를 내포한다.
- 즉, 모든 문서에서 자주 등장하지 않으면서 특정 단어들과 함께 등장하는 단어들은 서로 유사한 의미를 내포한다.
- 그러므로 단어의 조합인 문서는 의미가 있는 단어들의 비중에 따라 카테고리(Topic)가 결정된다.
우리는 이러한 컨셉의 프로세스에 따라 1.문서를 단어 조합으로 가공하고, 2~5.문서 내 각 단어들의 의미를 부여한 다음, 6.문서의 토픽을 결정해보도록 하자.
Step 2. 분석 대상(문서) 확인

분석 대상은 HuffPost의 뉴스데이터이며, 아래 캐글 링크에서 다운로드 받을 수 있다.
https://www.kaggle.com/datasets/rmisra/news-category-dataset
News Category Dataset
Identify the type of news based on headlines and short descriptions
www.kaggle.com

데이터(뉴스 정보)는 총 20만개, 카테고리는 42개이며 그 중 Politics가 가장 많은 데이터를 차지한다.

우리는 이렇게 이미 잘 나눠진 카테고리를 다시 한번 토픽모델링을 통해 세부 카테고리로 나눠볼 것이다. 분석하고자 하는 뉴스 카테고리를 하나 선정한 다음 요약 내용을 담고 있는 short_description 부분만 추출한다.
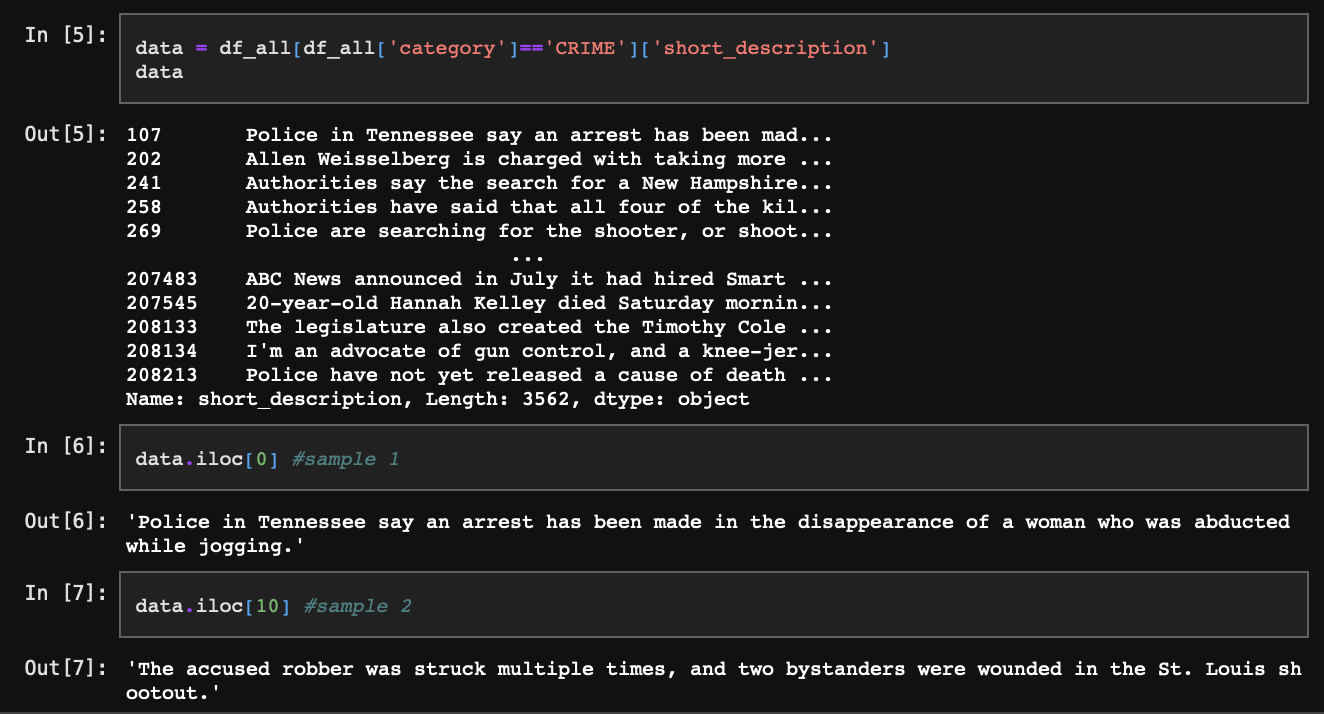
빈 값이 있다면 지워주자.
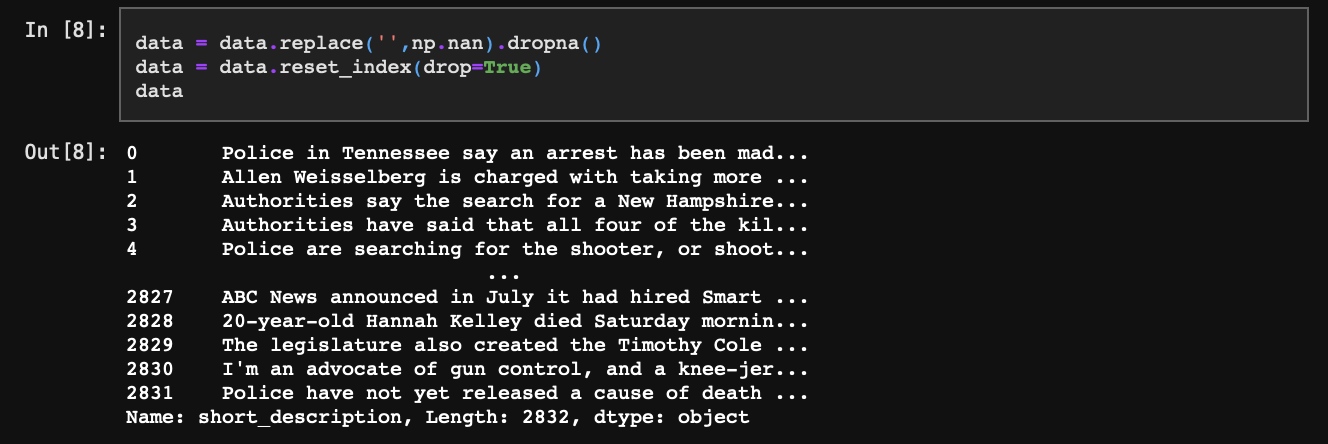
Step 3. 빈도 측면에서의 단어의 의미 부여(TF-IDF)
단어에 의미를 부여하는 방법은 다양하다. 어떤 방법이든 의미를 가지려면 단어를 숫자로 바꿔줘야 하며 이는 각 문서(short description)가 단어 벡터로 표현됨을 의미한다.
변환 방법은 대표적으로 Bag of Words, Word Embedding 방식이 있으며 우리는 Bag of Words, 그중에서도 TF-IDF(Term Frequency-Inverse Document Frequency) 방식을 사용한다. TF-IDF는 각 문장에서 출현하는 특정 단어 빈도인 TF(Term Frequency), 그리고 전체 문장에서 출현하는 특정 단어의 빈도인 IDF(Inverse Document Frequency)의 곱연산으로 정의되며, 이를 활용해 Step 1에서 소개한 토픽모델링 프로세스 중 2~5번 항목을 수행한다.
Word Embedding 방식이 각 단어별 잠재벡터(의미)를 즉시 부여한다면, TF-IDF는 단어의 출현 빈도와 비중을 토대로 문서의 잠재벡터를 추정한다. 따라서 엄밀히 말하면 TF-IDF는 각 단어가 그 자체로 의미를 지닐 수는 없으며 문장 내에서 혹은 토픽 내에서만 확률적으로 의미를 가진다.
3-1. TF
TF는 단순히 단어의 빈도를 의미한다. 따라서 CounterVectorizer() 함수 실행 결과값으로 함께 확인할 수 있다.
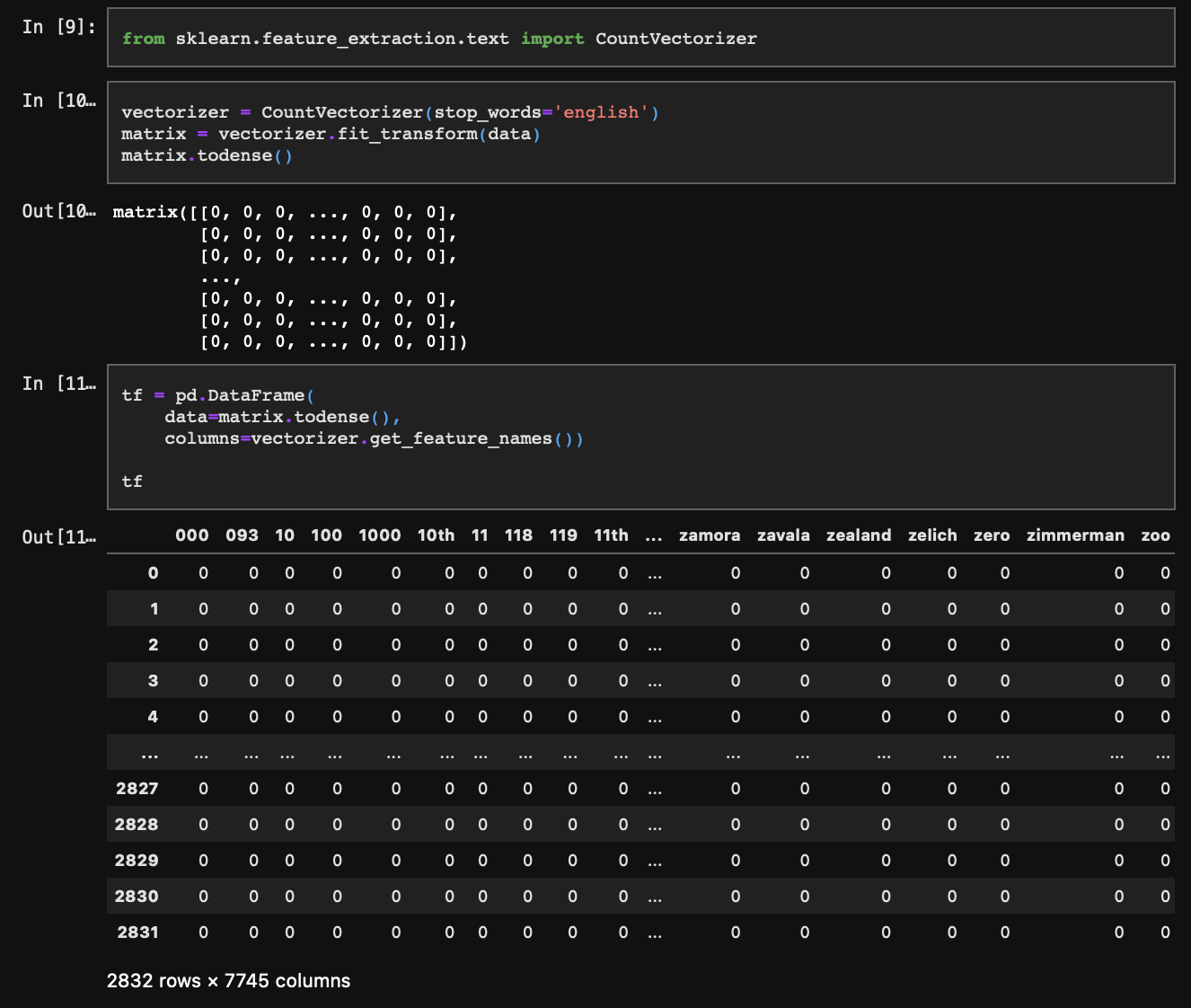
각 행(인덱스)은 문서를, 열(컬럼)은 단어를 의미한다. 각 데이터는 문서에 등장한 단어의 빈도가 되겠다.
여기서 연산량을 줄이기 위해 데이터를 일부 제거할텐데, 단어를 너무 적게 가지고 있는 문서(행)와 전체 문서상에 너무 적게 등장하는 단어(열)는 삭제해 주자. 물론, TF-IDF의 목적이 단어의 특수성과 보편성을 계산하기 위함인 것을 고려하면 원데이터로 분석하는 것이 가장 좋다.
- 단어를 너무 적게 가지고 있는 문서
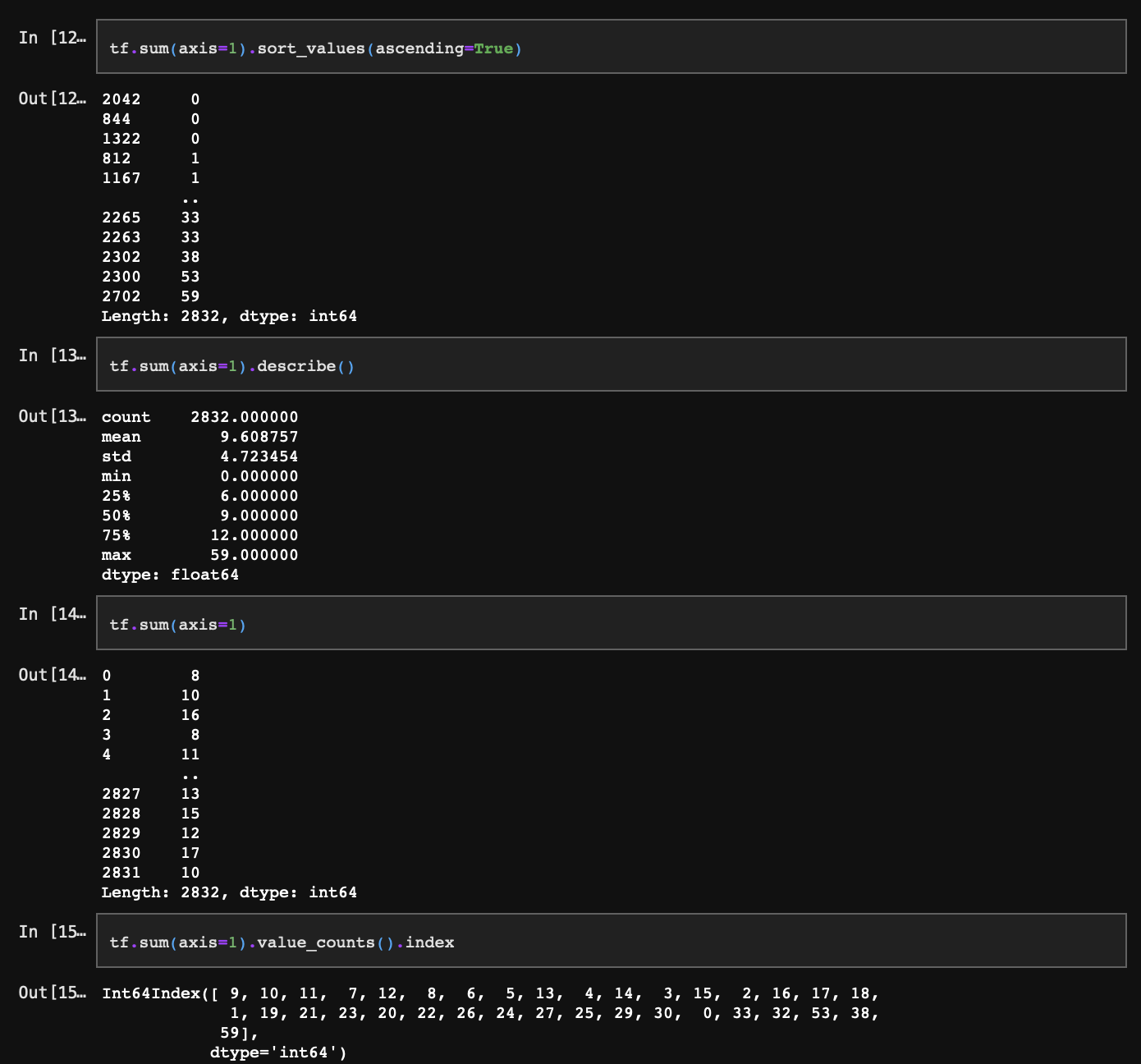
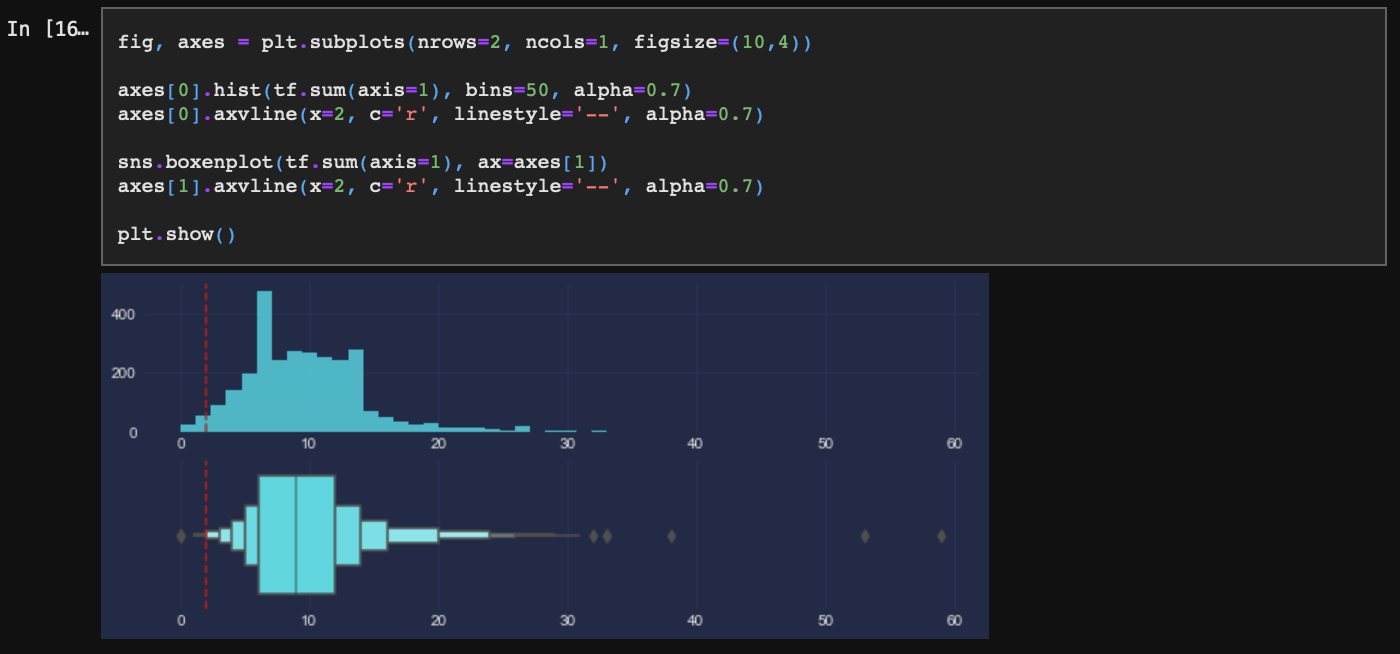
문장의 길이가 긴 것은 정보를 많이 포함하므로 문제되지 않는다. 단어 2개 이하로 구성된 너무 짧은 문장은 삭제한다.
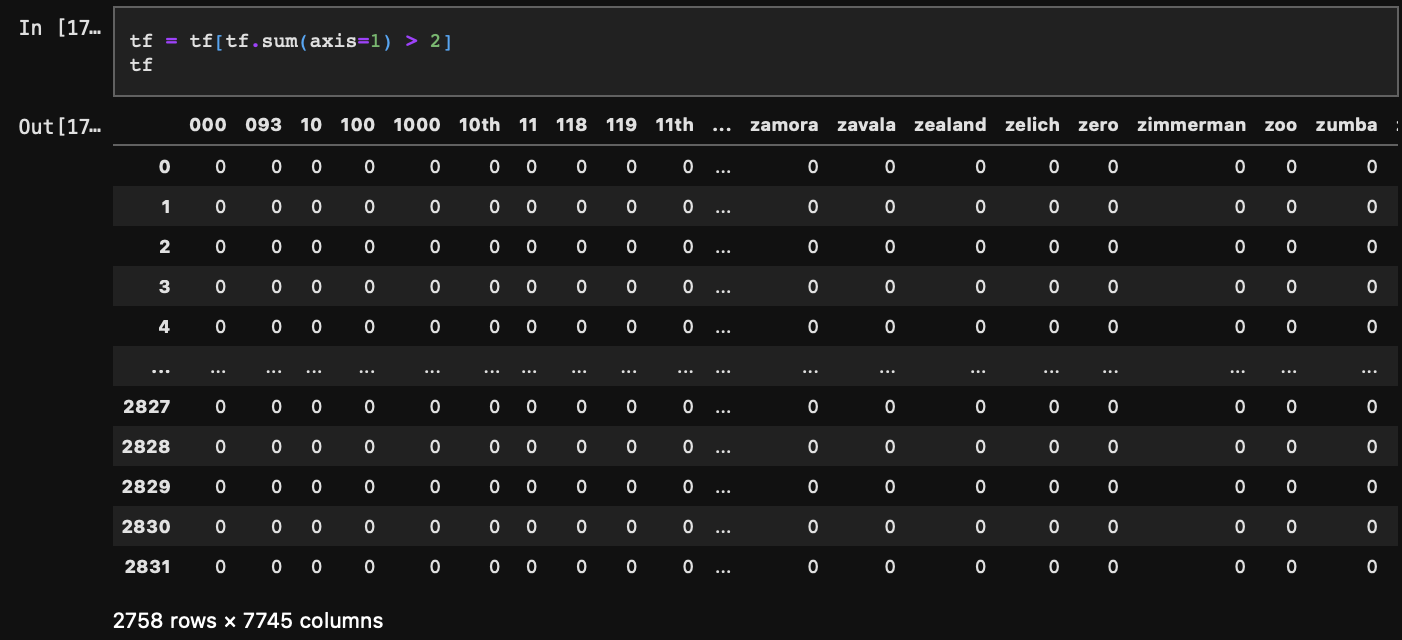
- 전체 문서상에 너무 적게 등장하는 단어
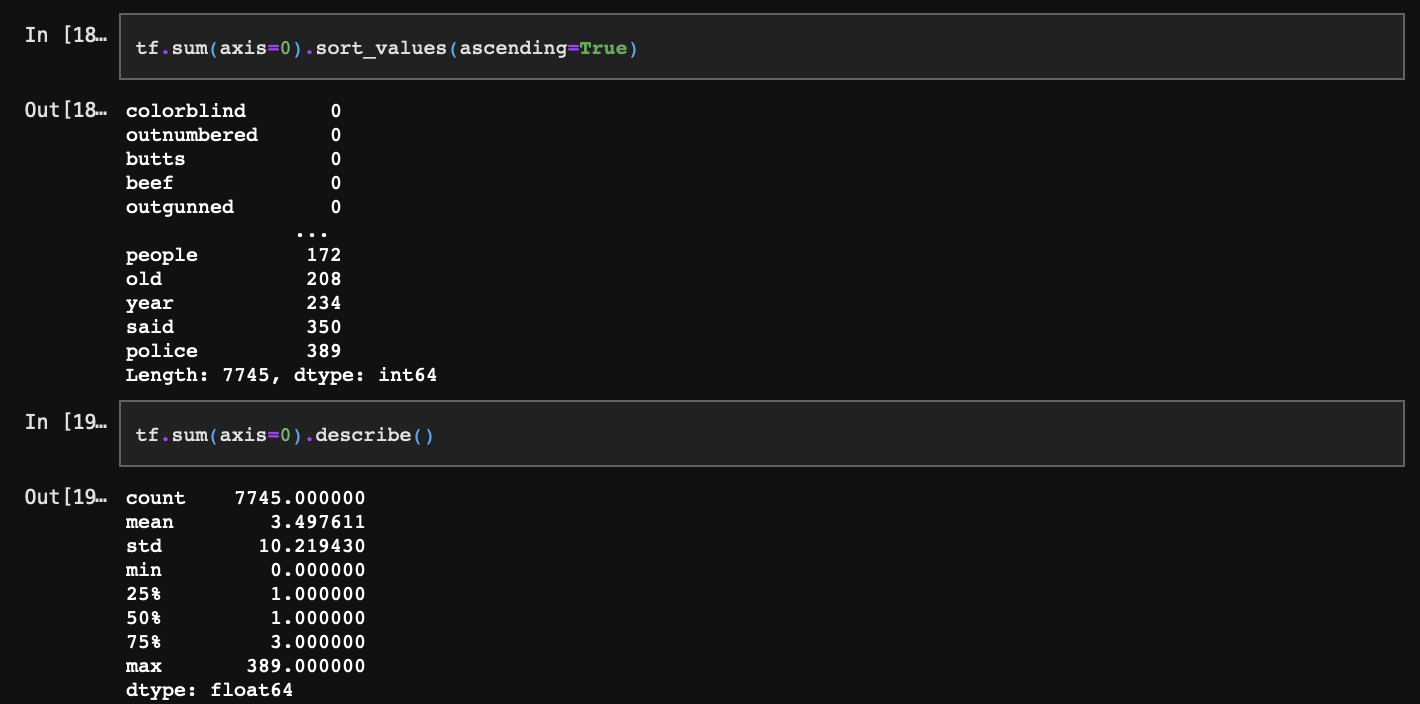
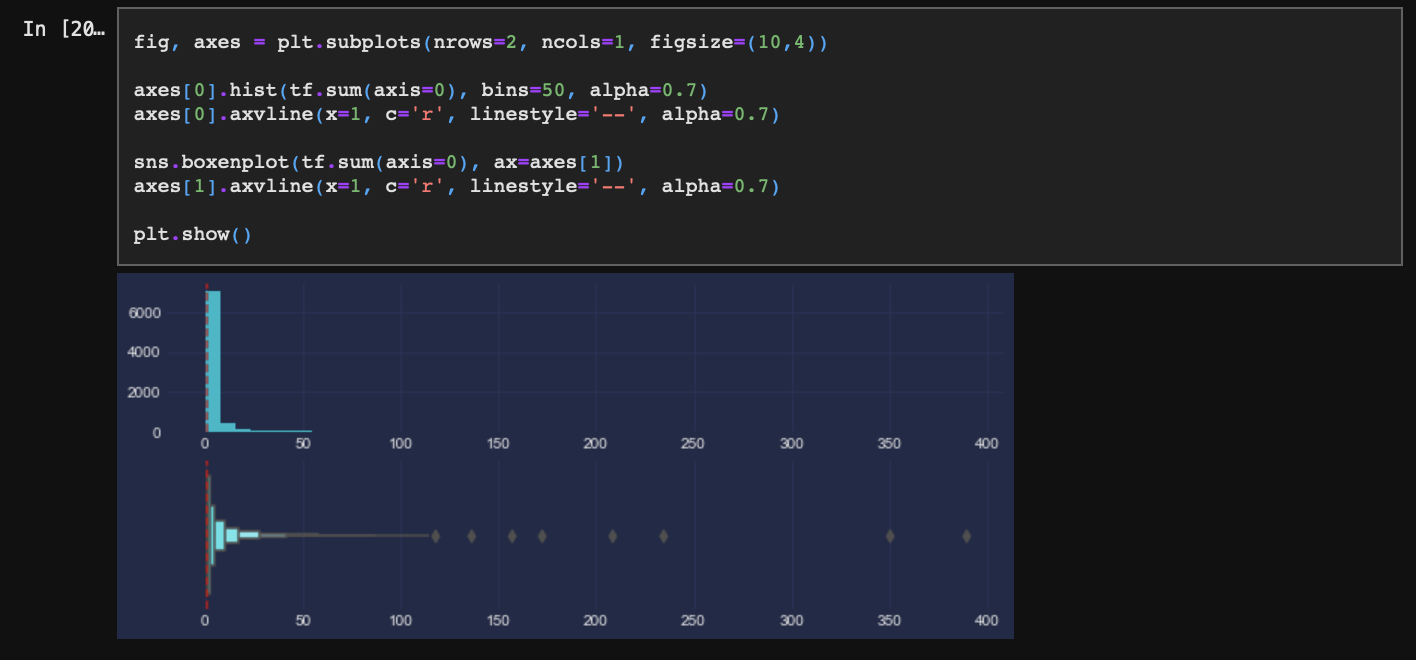
잘 보이지 않으니 x축을 확대해서 살펴보자.
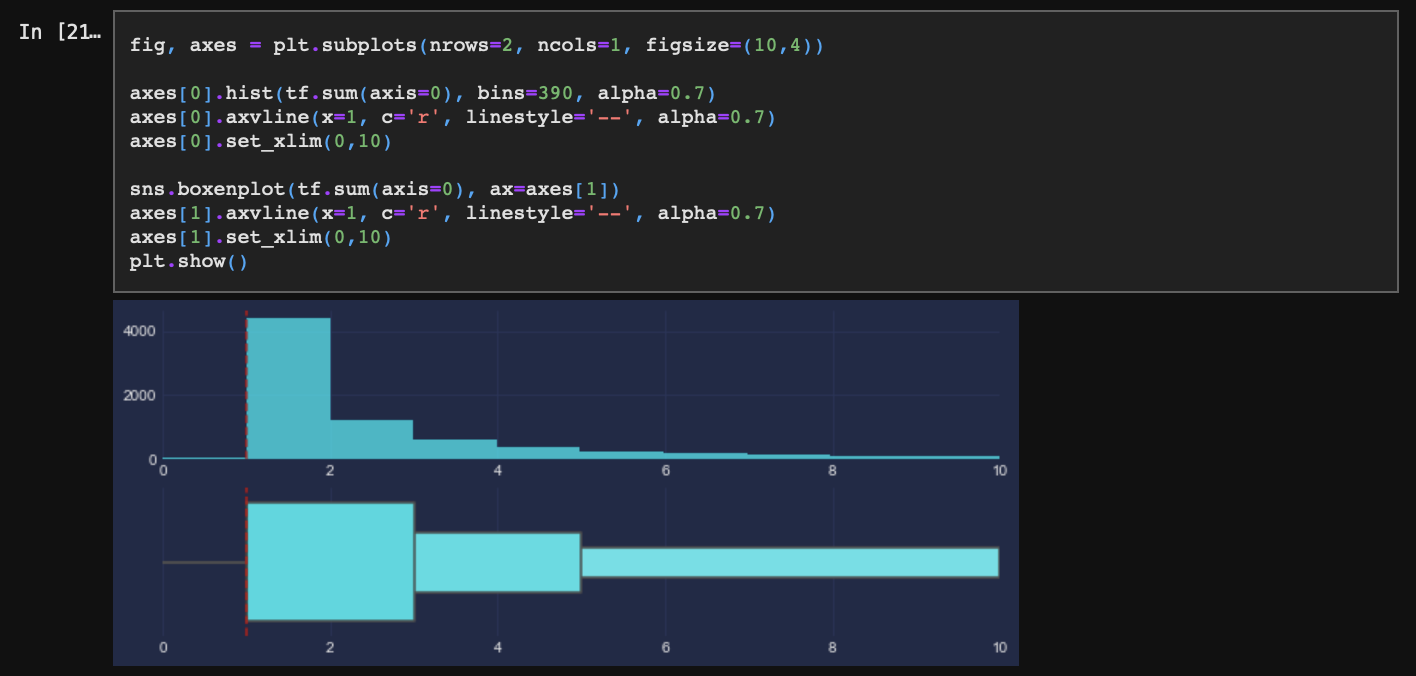
문서 1개에만 존재하는 단어 비중이 매우 크기 때문에 제거하기 어렵다. 따라서 최소 1개 문서에는 출현하는 단어는 모두 단어 사전에 포함하는 것이 좋다.(단어는 사실 앞에서 너무 짧은 문장을 제거했을 때 발생된 데이터다. 따라서 이는 제거해주는 것이 맞다.) 그러나 실습의 편의를 위해 최소 2개의 문서에는 출현하는 단어만 단어 사전에 포함하도록 하자. 연산 속도를 높이기 위함이다.
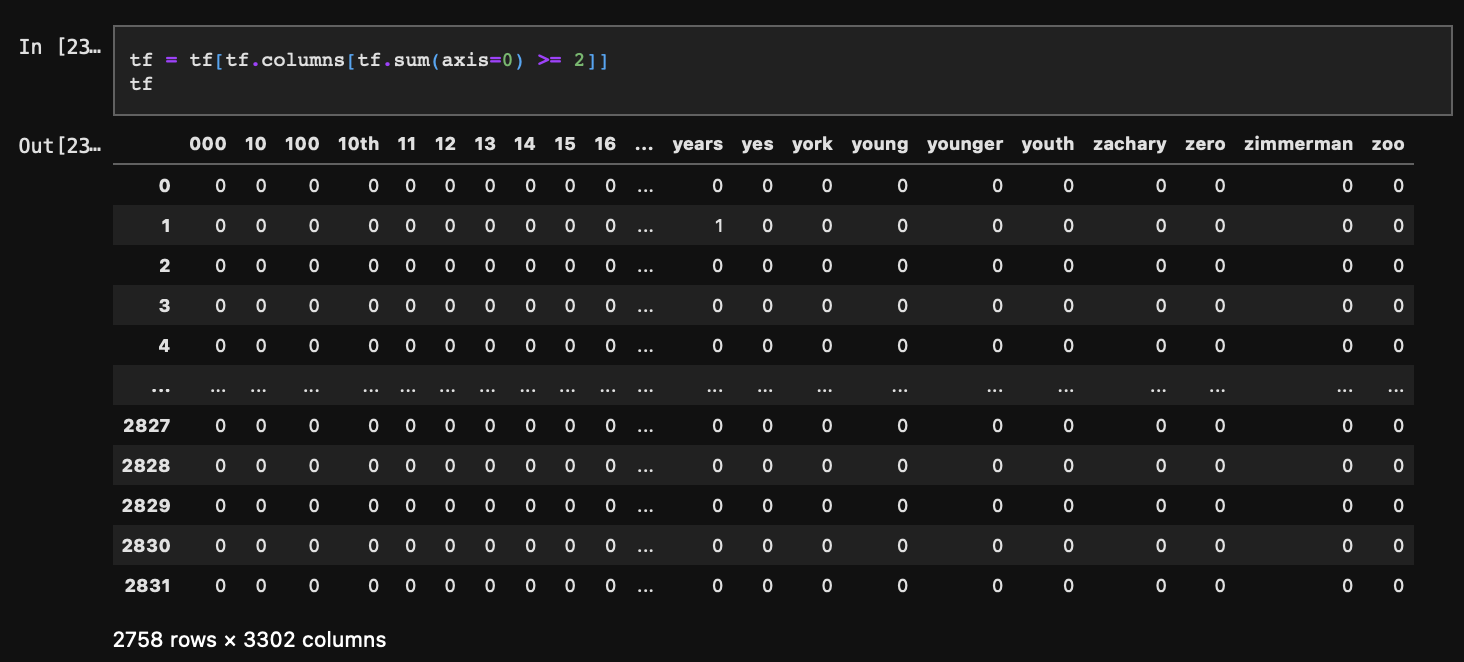
마지막으로 컬럼 중에 숫자로만 구성된 것들도 제거해주자.
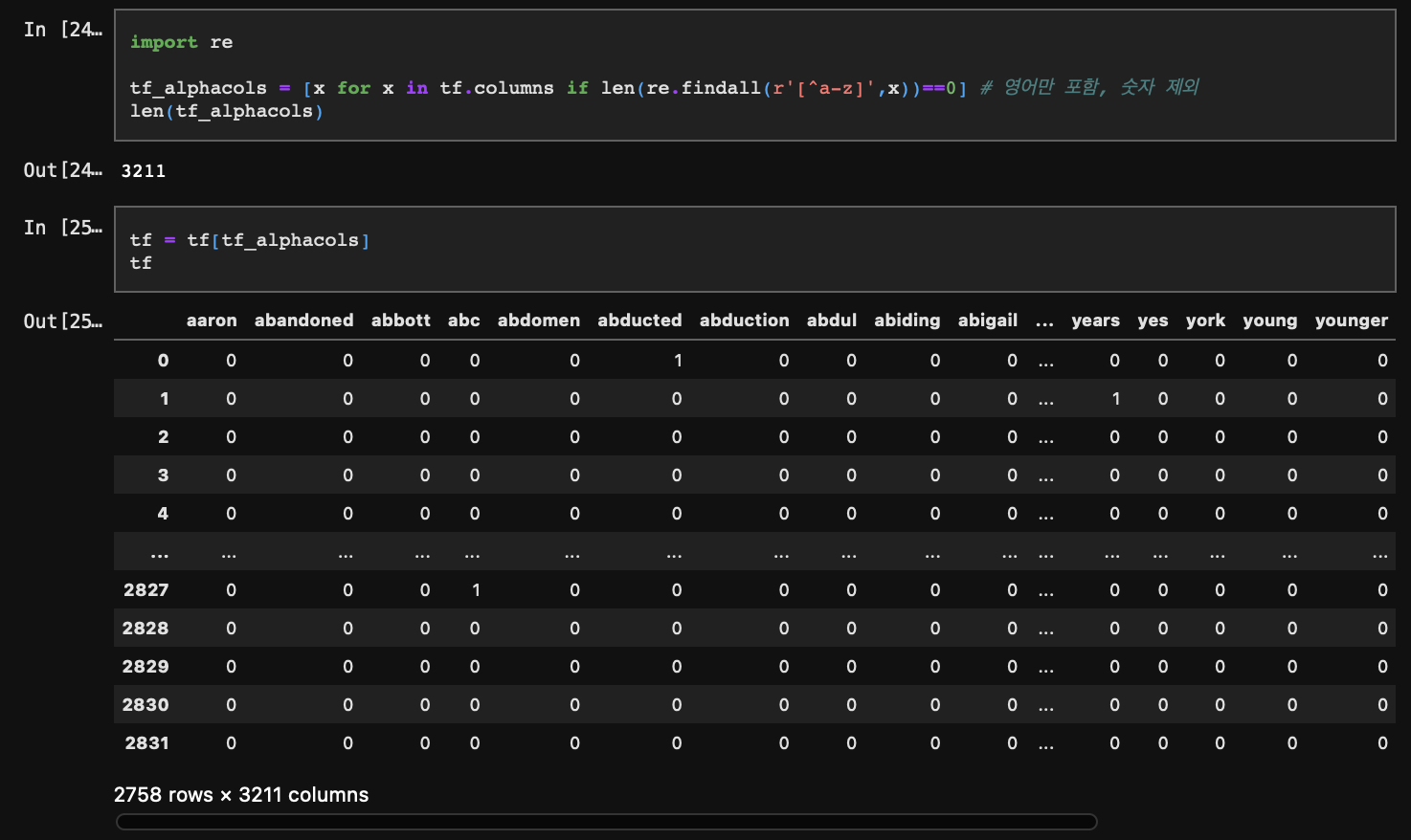
이렇게 TF-IDF 중 TF(문서별 단어 빈도) 구성을 완료했다.
3-2. IDF
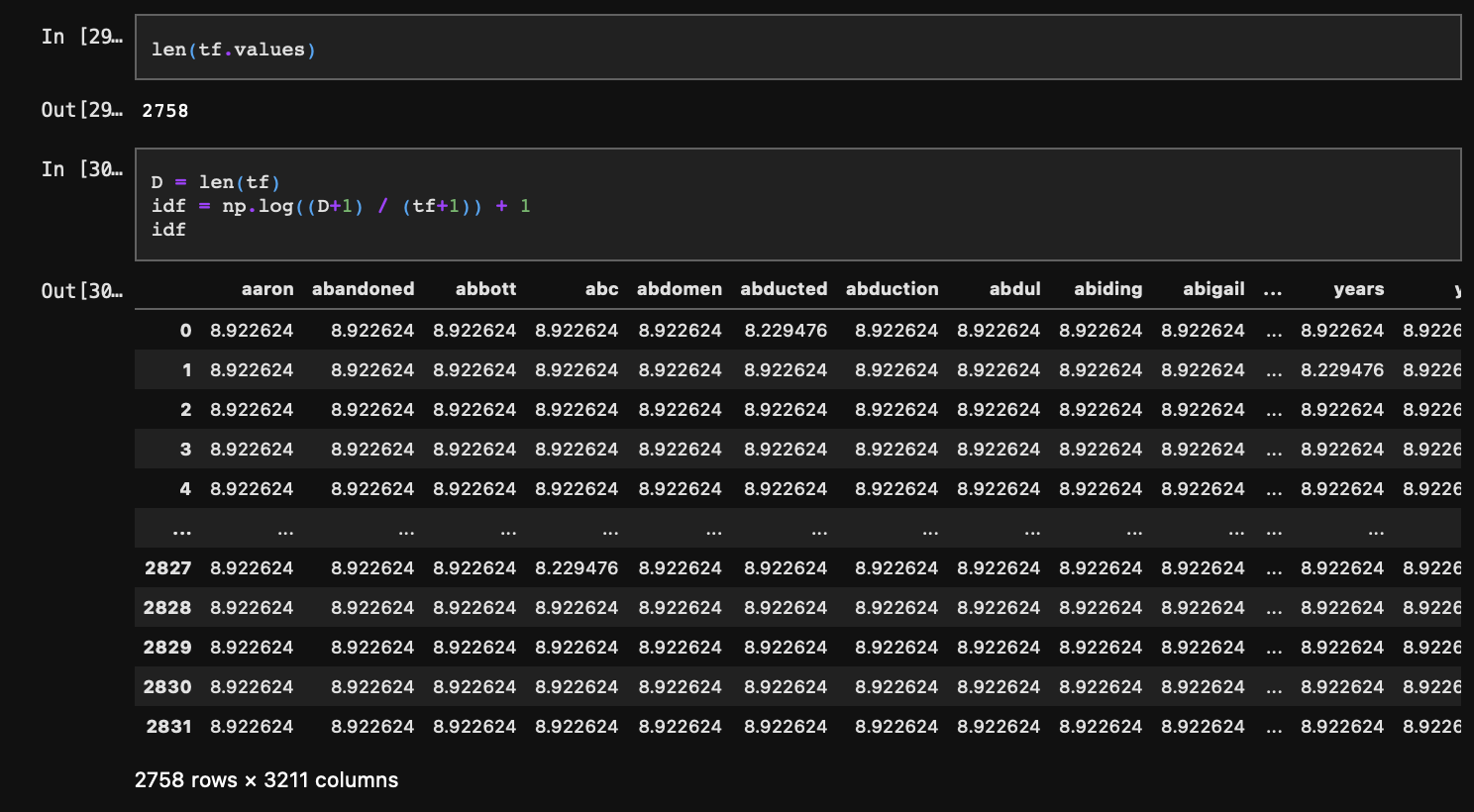
IDF는 DF의 inverse값이다. DF는 특정 단어가 출현하는 문서의 수를 의미한다. 따라서 전체 빈도의 합계와는 차이가 있다.
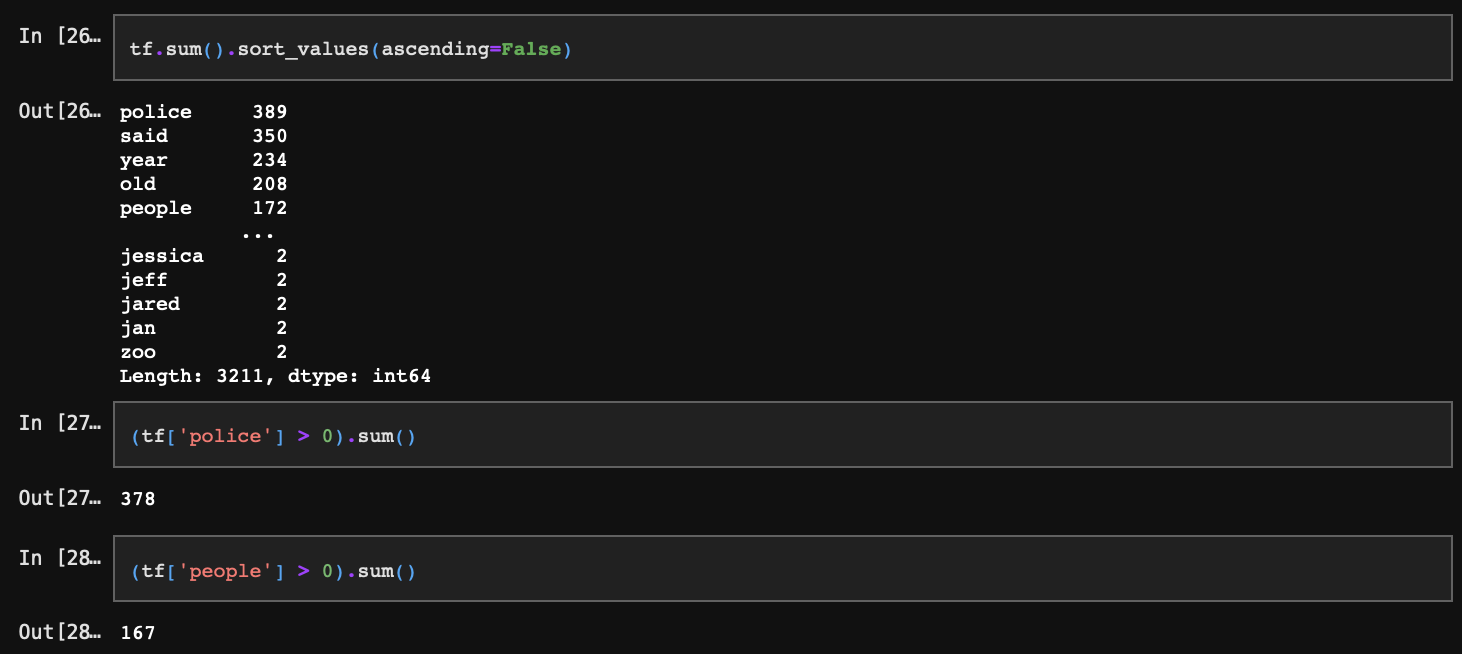
이러한 특정 단어가 출현하는 문장의 수, 즉 DF의 역수를 취해주면 IDF가 되는데 이때의 역수는 단순히 1/DF를 의미하는 것은 아니다.
총 문서의 수 + 1을특정 단어를 포함하는 문서의 수 + 1로 나누고 로그를 취한 다음 다시 1을 더해준다.
이렇게 하는 이유는 다음과 같다.
- 분자 혹은 분모가 0이 되지 않도록 총 문서의 수, 특정 단어를 포함하는 문서의 수에 각각 1을 더한다.
- 바로 위 셀에서 처럼 특정 단어를 포함하는 문서의 수가 총 문서의 수 대비 매우 적을 수 있다. 따라서 로그를 취해 분포가 너무 커지지 않도록 스케일을 줄여준다.
- 또 반대로 만약 대부분의 문서에 특정 단어가 포함되는 경우 자연로그를 취한 값은 0에 수렴할 것이다. IDF는 TF에 곱해지는 가중치로써 역할을 해줘야 하기 때문에 1을 더해준다.
이렇게 해당 문서에 등장한 특정 단어가 희소할 경우 가중치를 크게, 빈번할 경우 가중치를 낮게 반영한다.
3-3. TF-IDF
앞에서 구한 tf와 idf를 곱해주면 TF-IDF가 된다. 즉, 각 문서별 특정 단어의 빈도가 TF인데 여기에 해당 단어가 얼마나 특수한가에 대한 정보(IDF)를 가중치로 곱해주는 것이다.
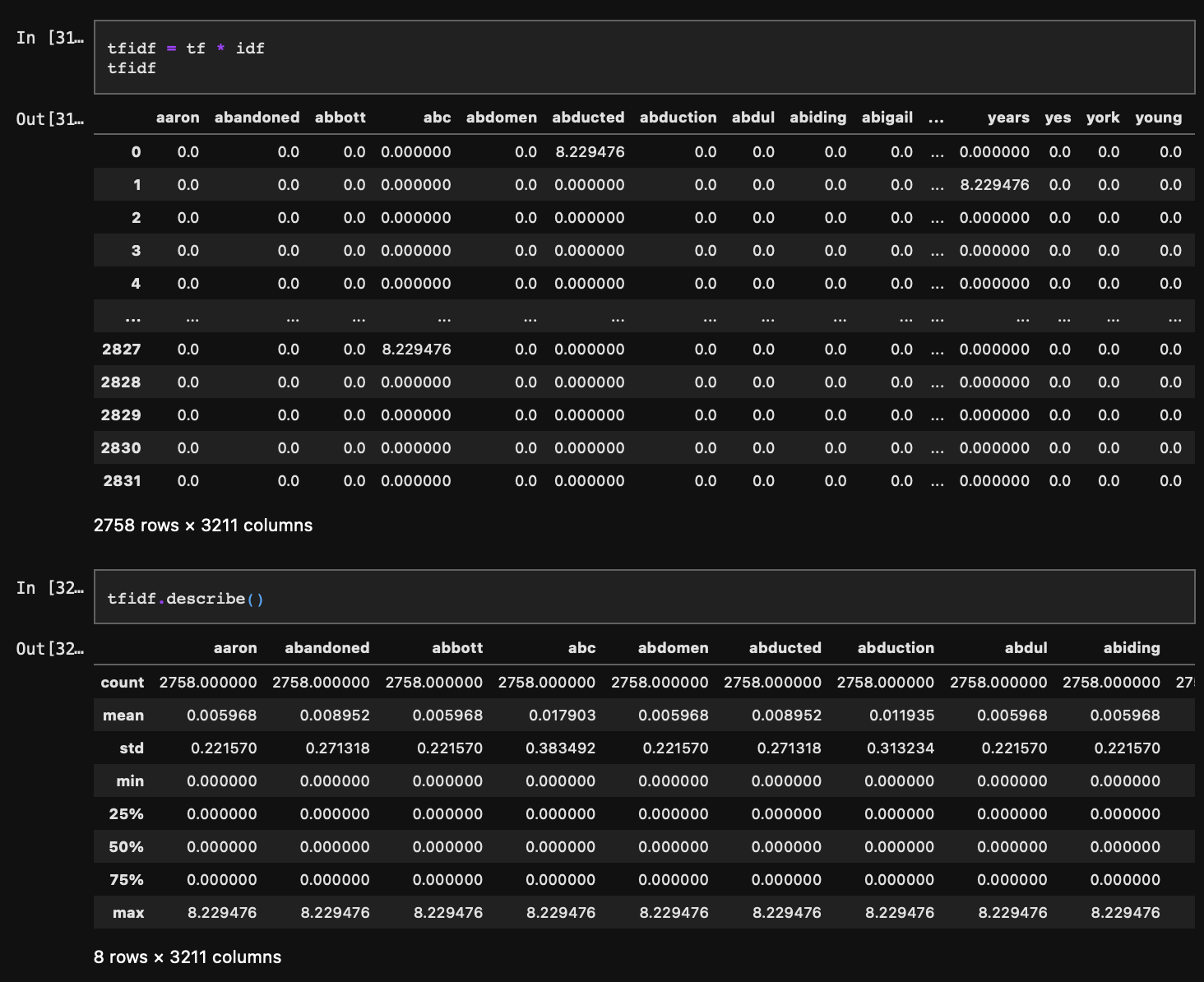
분포를 보면 대부분의 값이 0으로 최댓값과 차이가 있다. 이는 너무 넓은 범위에 sparse 한 데이터가 찍혀있는 것이므로 데이터를 한번 더 밀집 공간 내 압축해 줄 필요가 있다.
따라서 각 단어의 고유속성, 즉 단어 벡터크기(원점으로부터의 길이)를 나눠주자. 예를 들어 첫 번째 단어의 경우 벡터크기는 다음과 같다.

이를 전체에 적용하여 모든 단어의 벡터 길이를 구하고, 이렇게 구한 벡터 길이로 단어별 빈도데이터를 나눠주면 분포는 다음과 같이 바뀐다.
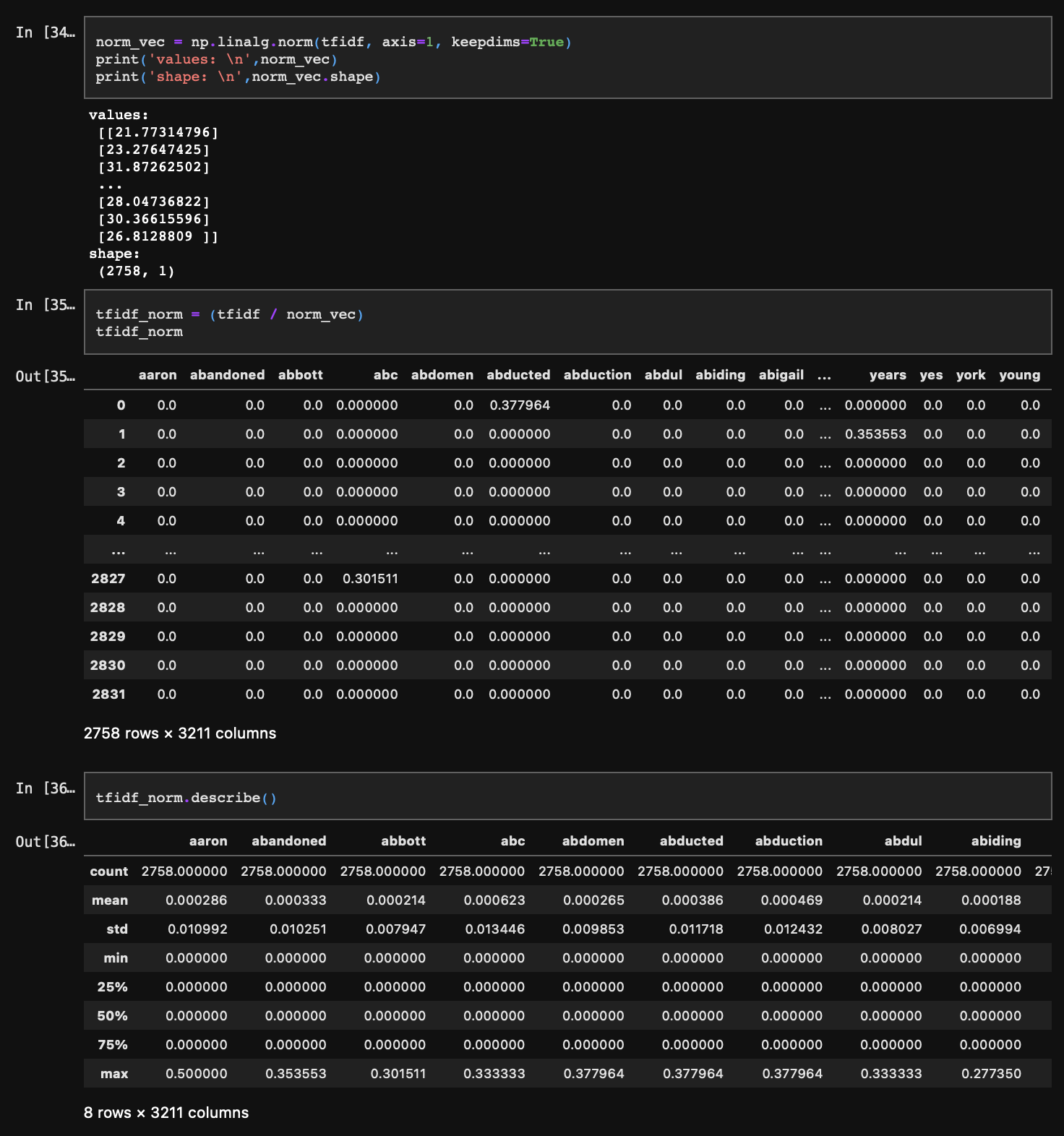
Step 4. 토픽 추출
사실, 토픽모델링의 경우 LDA(Latent Dirichlet Allocation)가 대표적이지만 본 실습에서는 빈도 기반의 TF-IDF 행렬에서 어떻게 잠재의미를 추출해 낼 수 있는가?를 분석해보기 위해 LSA(Latent Semantic Analysis) 방법론을 사용하고자 한다.
LSA는 SVD 행렬분해(특이값 분해)를 통해 추출한 대각행렬(특이값 행렬)에서 정보량이 많은(값이 큰) 부분을 추출해 최소한의 차원(벡터)으로 토픽을 구성하는 방법론이다. 따라서 SVD를 1차 수행한 후 정보량이 많은 부분행렬을 추출하는 방식으로 LSA를 구현해보도록 하자.
먼저, SVD를 수행하기 전에 np.inf(무한대), 혹은 np.nan(계산불가) 값이 있는지 확인해야 한다. 넘파이 연산 시 실수를 0으로 나누면 inf 값을, 0을 0으로 나누면 NaN값을 반환하게 되는데, 앞서 충분히 많은 0의 극한값들을 서로 연산했기 때문에 문제 가능성이 있다.
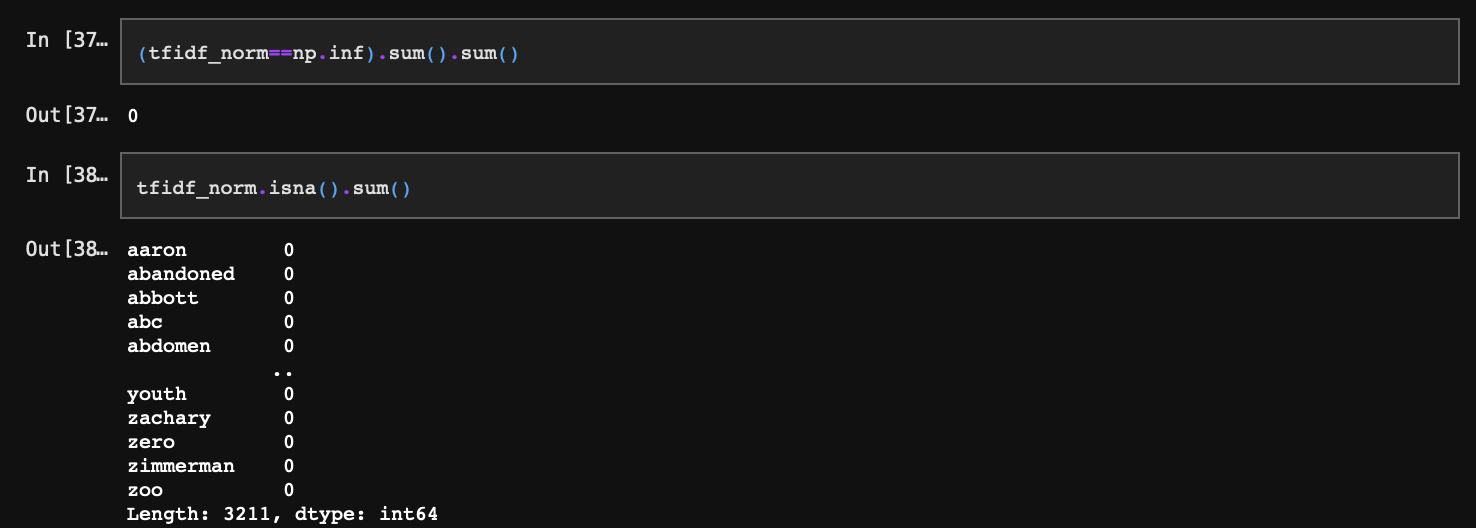
NaN값들이 확인되었다. 해당 행을 제거한다.
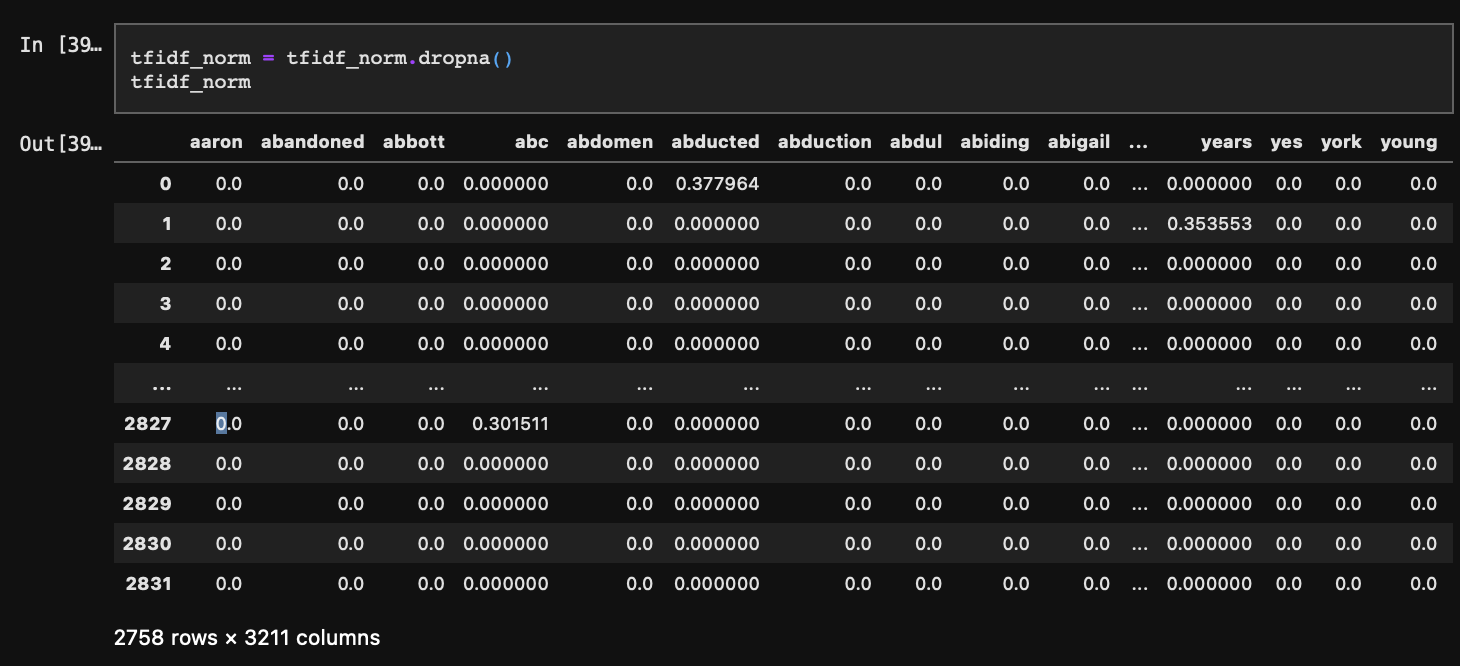
4-1. SVD
SVD(Singular Value Decomposition)는 A=(M x N) 행렬을 U=(M x M), S=(M x N), VT=(N x N) 3개의 행렬로 분해한다.
여기서 U는 직교행렬, VT 직교행렬을 transpose 시킨 전치행렬, S는 직사각 대각행렬이다. 이때, A=U*S*VT에서 양 변에 V를 곱하면 AV=US가 된다. 이 식의 의미는 직교행렬 V를 A행렬로 선형변환했을 때, 각도는 동일하고 길이만 다른 직교행렬 U*S가 된다는 것이다. 이러한 작용의 의미, 혹은 과정이나 맥락을 이해하기 위해서는 먼저 선형대수의 관점에서 직교행렬 및 단위행렬의 성질을 이해할 필요가 있다. 그러나 우리는 결과적으로 이 식을 구함으로써 어떤 이점이 있는가에 초점을 맞추도록 하자.
A=USVT의 식으로 다시 돌아와 보면, S가 어떤 값을 가지든 U의 행(M)과 VT의 열(N)이 A의 그것(M x N)과 동일해야 함을 알 수 있다. 만약 S=(1 x 1)이라면, U=(M x 1), VT=(1 x N)이 되어야 하고, S=(2 x 100)이라면, U=(M x 2), VT=(100 x N)이 되어야 한다. 여기서 불변하는 것은 M과 N이다. 그리고 A가 (문서 x 단어)의 행렬이므로 M=문서, N=단어가 된다. 문서는 단어벡터로 이루어져 있었다. 즉, 단어->문서로 즉시 이어지던 관계를 단어->[잠재벡터]->문서로 한 단계를 더 넣은 것으로 이해해 볼 수 있다. 이 잠재벡터가 바로 토픽이며, 단어 조합을 문장으로 만들어주는 어떠한 정보를 내포하는 것이다.
결과적으로 S는 토픽 정보를 가지고 있는데 그 크기는 (1 x 1)부터 (M x N)까지의 자유도를 가진다. 이때, 자연스럽게도 S가 (1 x 1) 일 때나 (M x N) 일 때나 모두 U*S*VT는 A의 형태는 갖춰야 하기 때문에 S가 아무리 작아도(S=(1 x 1)) 최소한의 정보는 가지고 있을 것이라 생각해 볼 수 있다. 실제로 S의 대각 원소의 값은 좌상단부터 우하단까지 내려갈수록 작아진다. 즉, S의 대각 원소 첫 번째 값이 가장 중요한 정보를 가지고 있고, 가장 마지막 값이 가장 작은 정보를 가지는 것이다. 따라서 우리는 SVD를 수행해 S를 구함으로써 A가 구성되기 위해 가장 중요한 정보부터 가장 중요하지 않은 정보까지의 값을 확인할 수 있게 되는 것이다.
SVD는 넘파이 선형대수 패키지를 통해 간단히 수행할 수 있다.
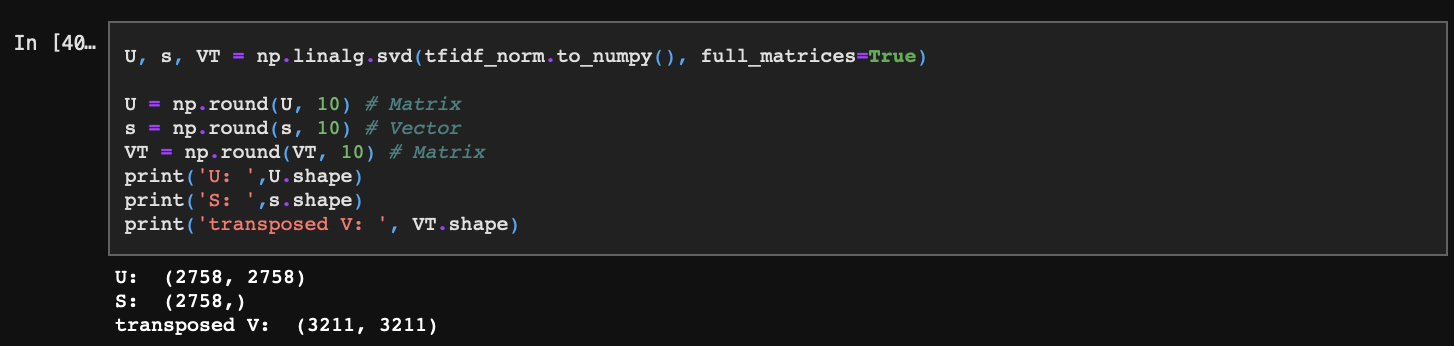
4-1. S
잠재벡터 s를 먼저 확인해 보자. svd() 함수를 사용하면 s는 벡터로 추출된다. 이 벡터의 첫 번째 값이 가장 크고, 마지막 값으로 갈수록 가장 작아지는 것을 확인할 수 있다. 이것이 각 토픽의 정보량이 된다.
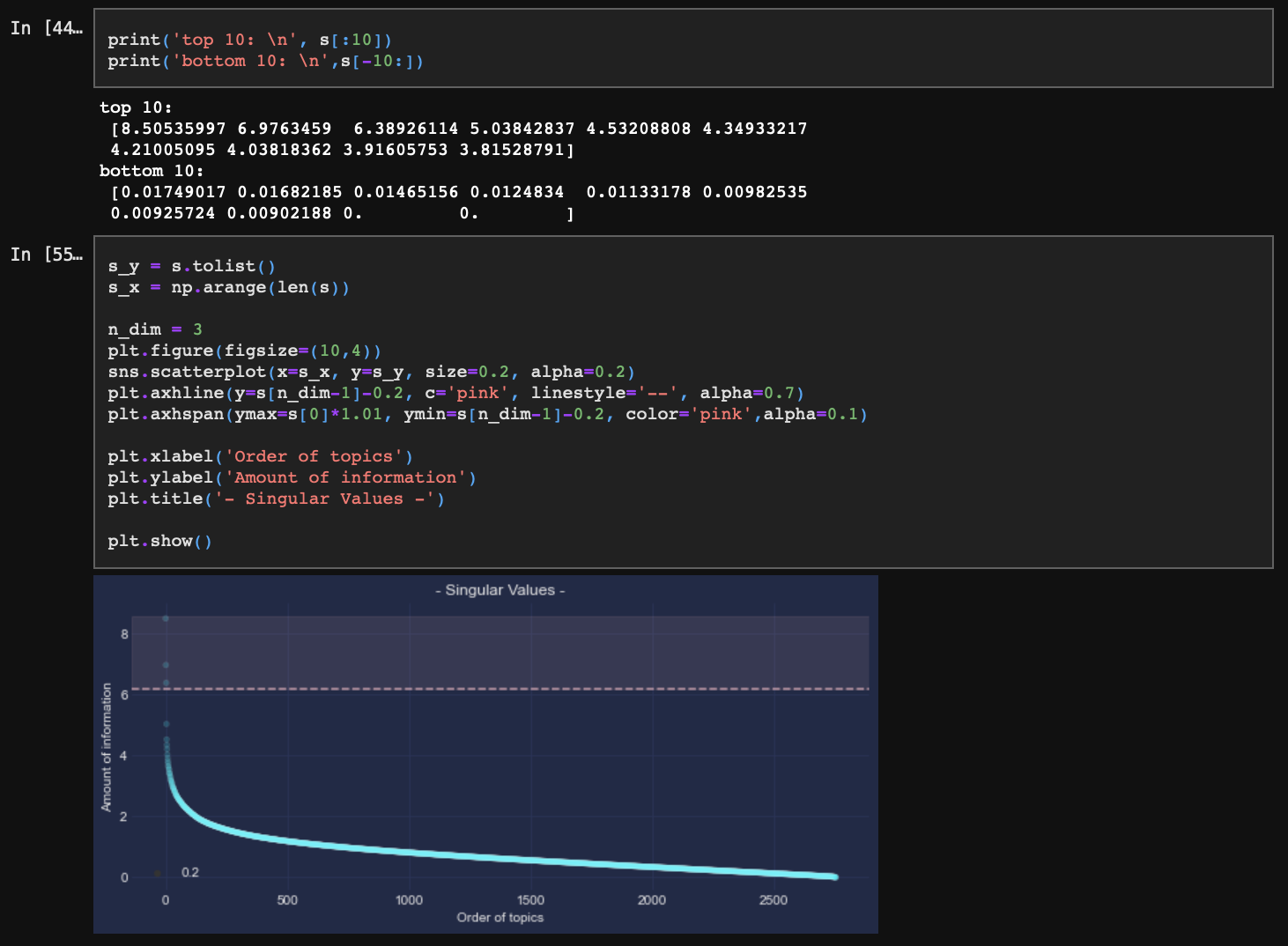
차트에서 붉은 영역에 속한 점들이 가장 설명력이 높은 상위 3개 토픽을 표시하고 있다. 이 3개 토픽만 활용해 문서의 주제를 분석한다.
참고로 잠재벡터를 다음과 같이 대각행렬로 표현해 줄 수도 있다.
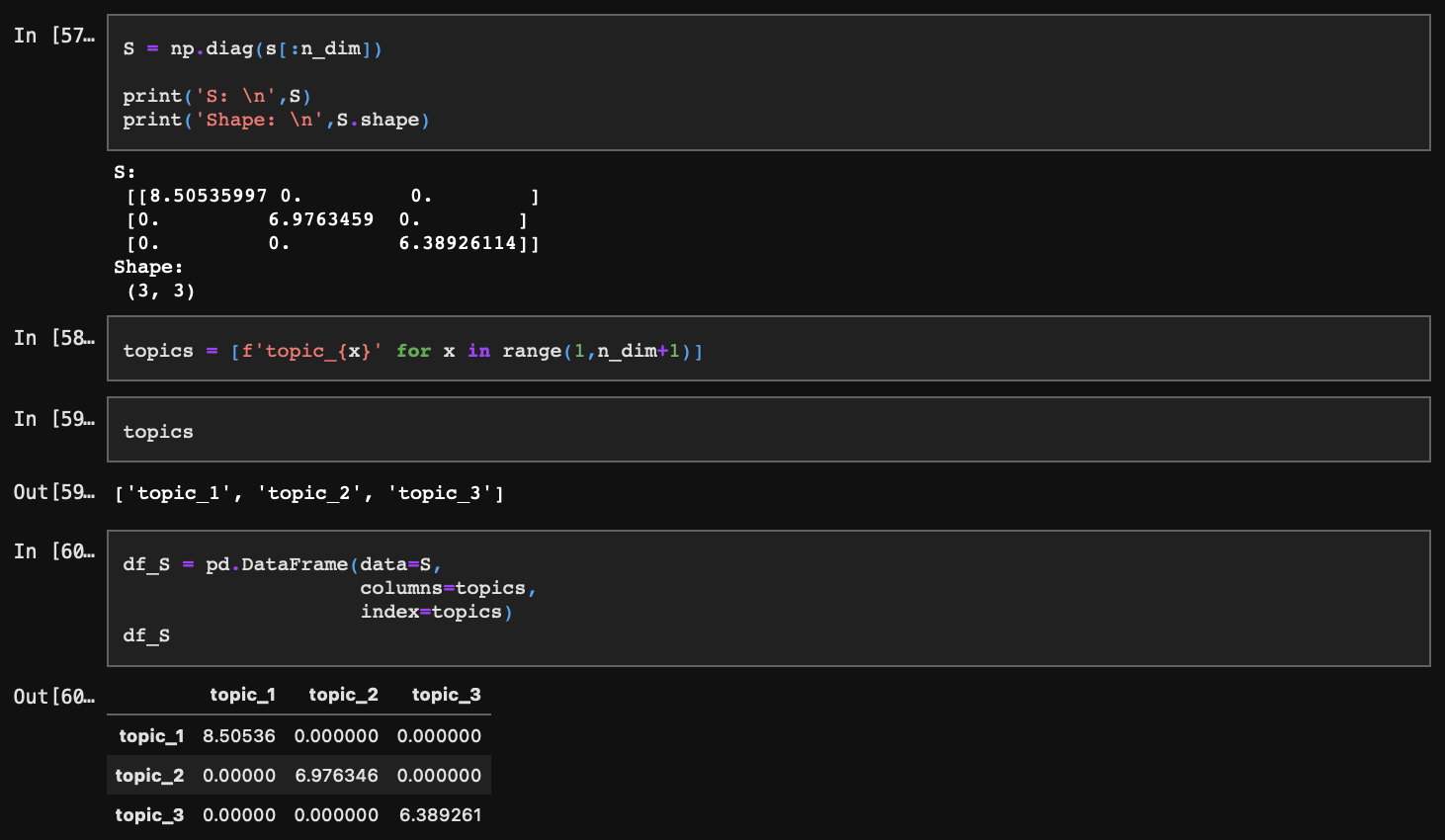
4-2. U
U는 문서가 전체 토픽마다 일치하는 확률을 담고 있다. 특이값 s의 크기 3에 맞춰 열을 잘라주면 가장 설명력(정보량)이 높은 3개 토픽에 대한 확률만 추출된다.
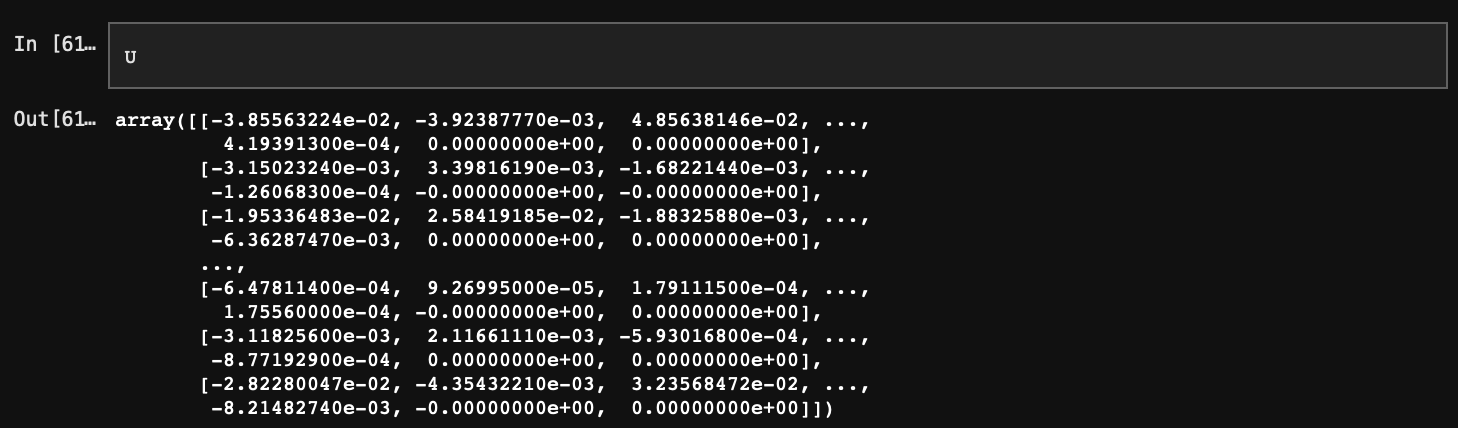
U를 데이터프레임으로 변환해줄 텐데, index를 기존 문서 인덱스에 맞게 지정해주는 것이 중요하다.
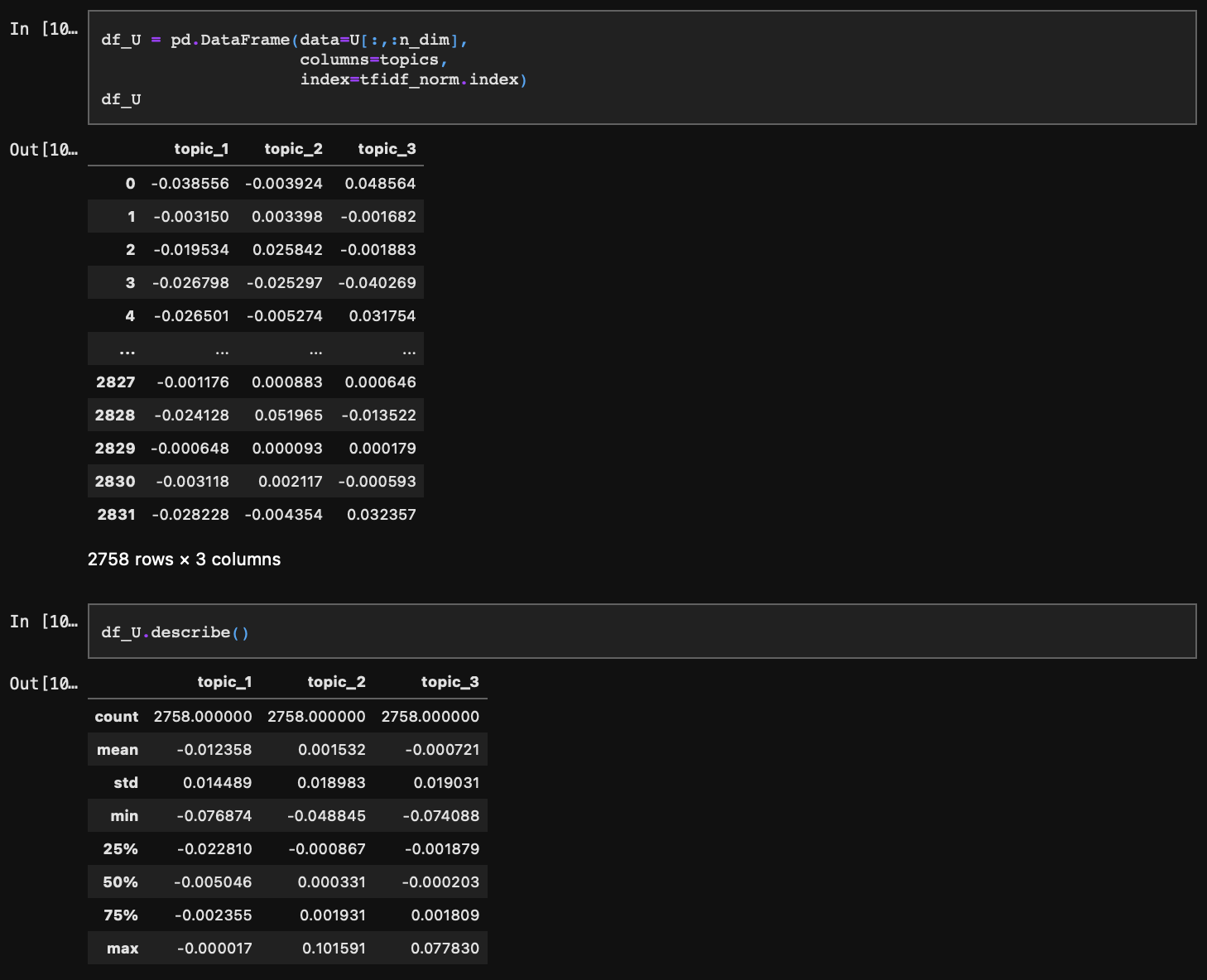
아래에서 시각화를 해줄텐데, X, Y, Z 좌표 범위를 0~1로 동일하게 맞추기 위해 스케일링을 미리 수행해주겠다.
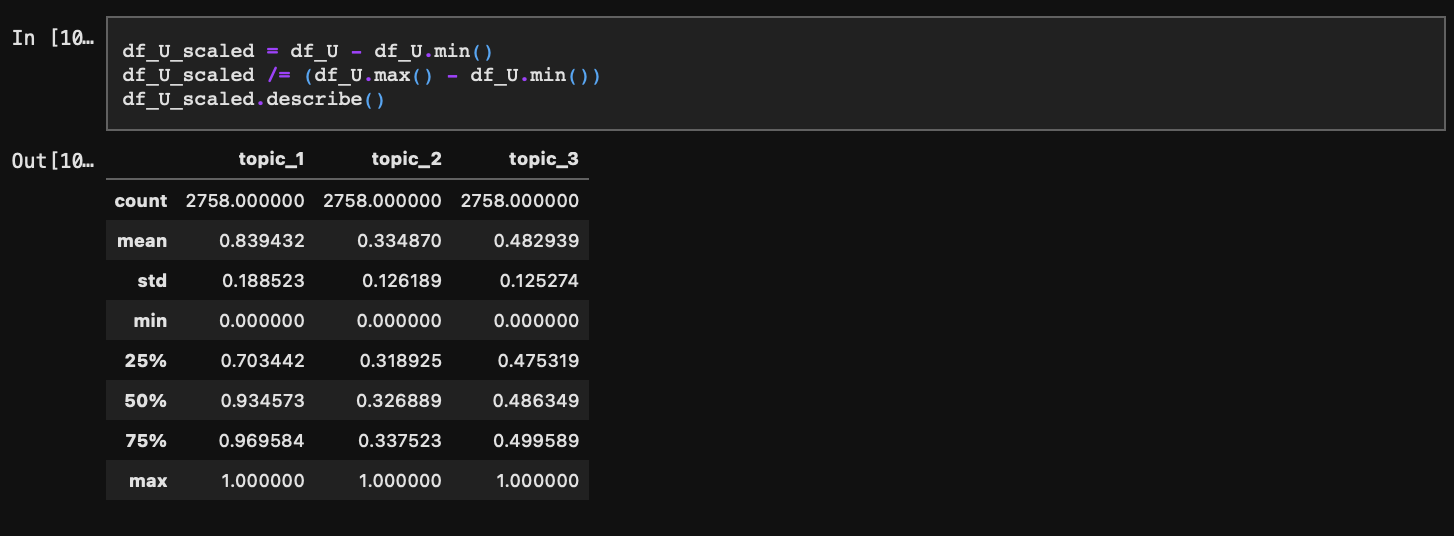
4-3. V
마지막으로 V는 각 단어가 각각의 토픽마다 일치하는 확률을 담고 있다. VT를 특이값 s의 크기 3에 맞춰 행을 잘라주면 가장 설명력(정보량)이 높은 3개 토픽에 대한 확률만 추출되고 이를 Transpose 시키면 V를 구할 수 있다.
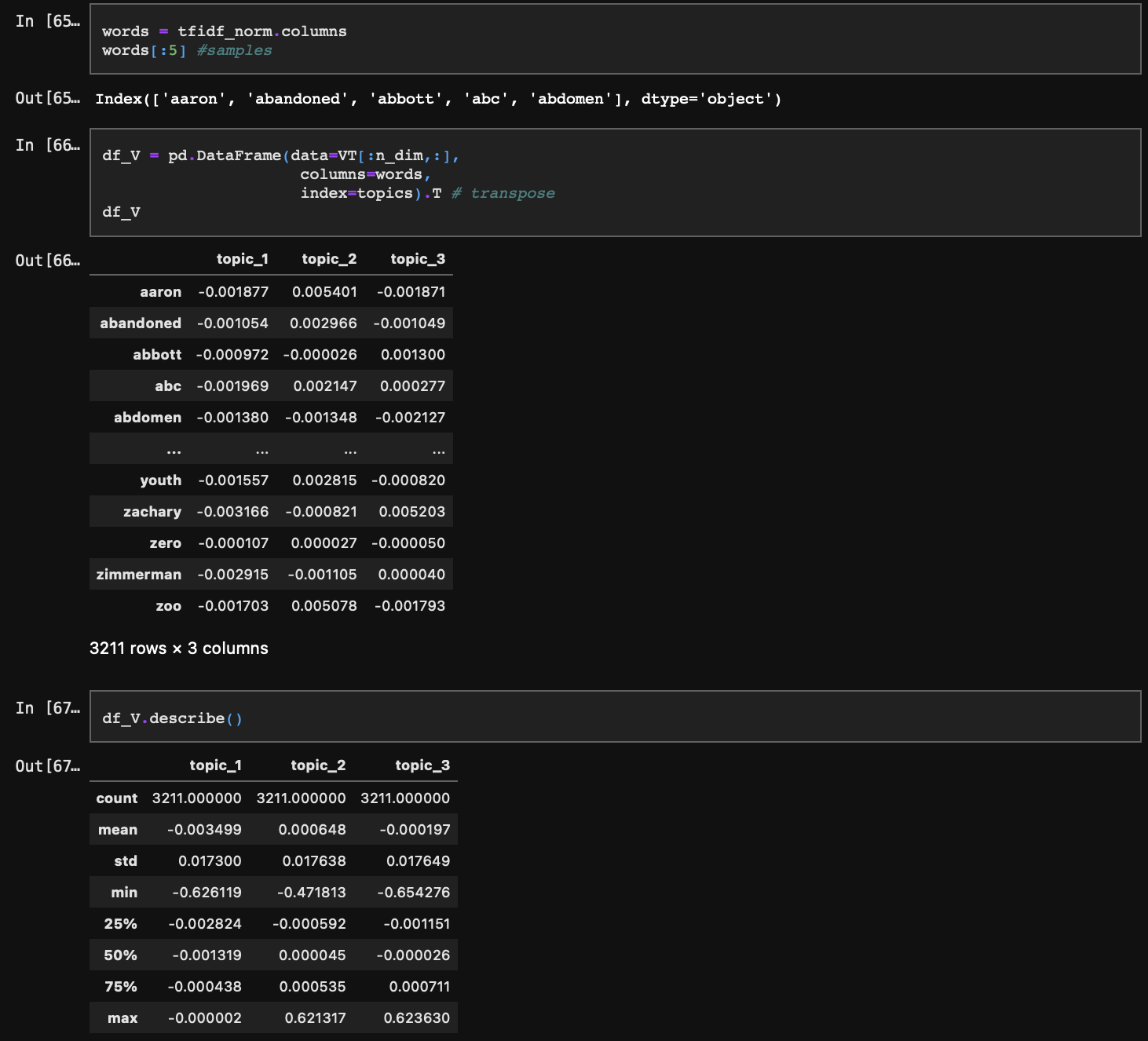
V도 마찬가지로 시각화를 위해 스케일링을 진행하자.
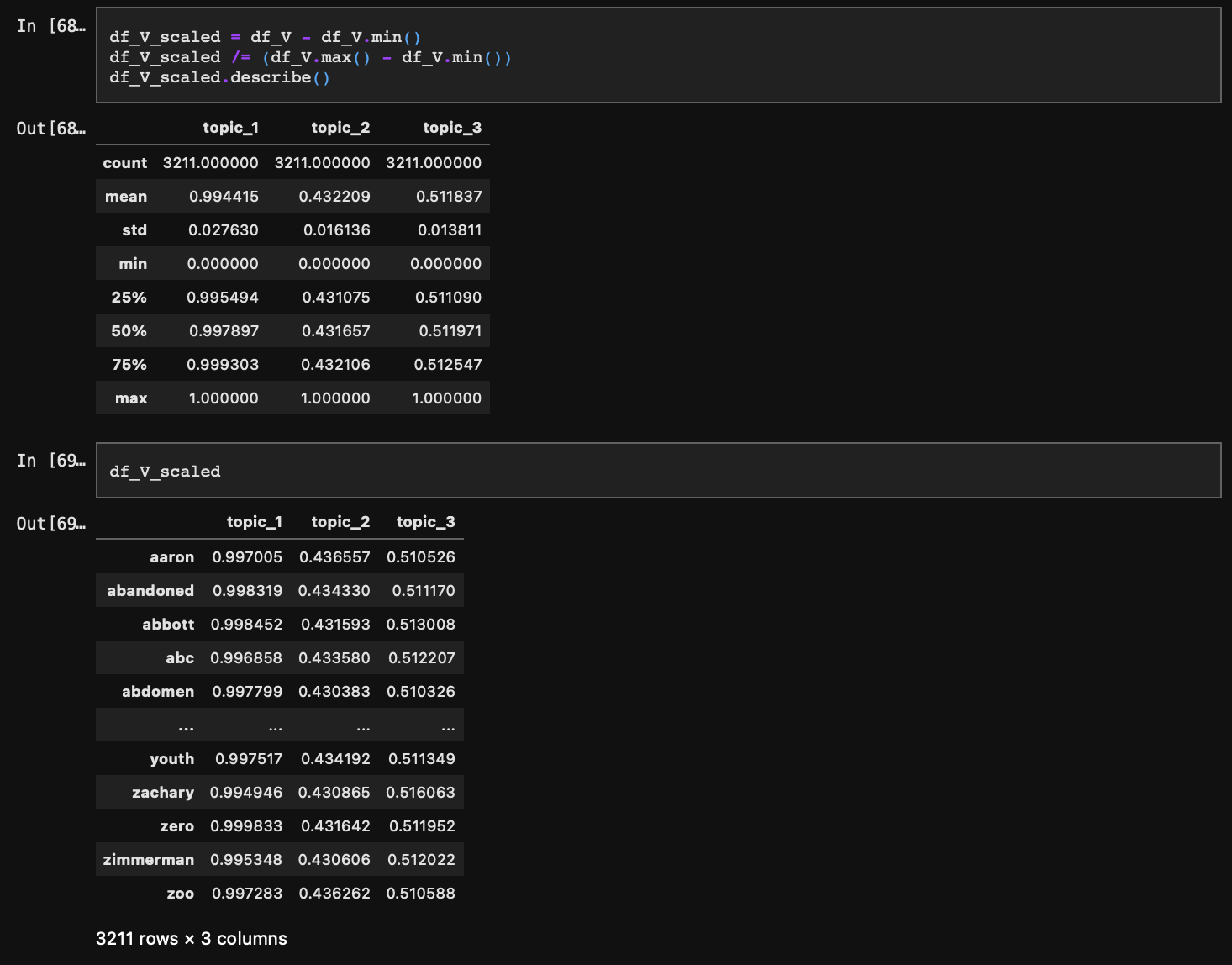
4-4. 각 토픽에 해당하는 확률 시각화
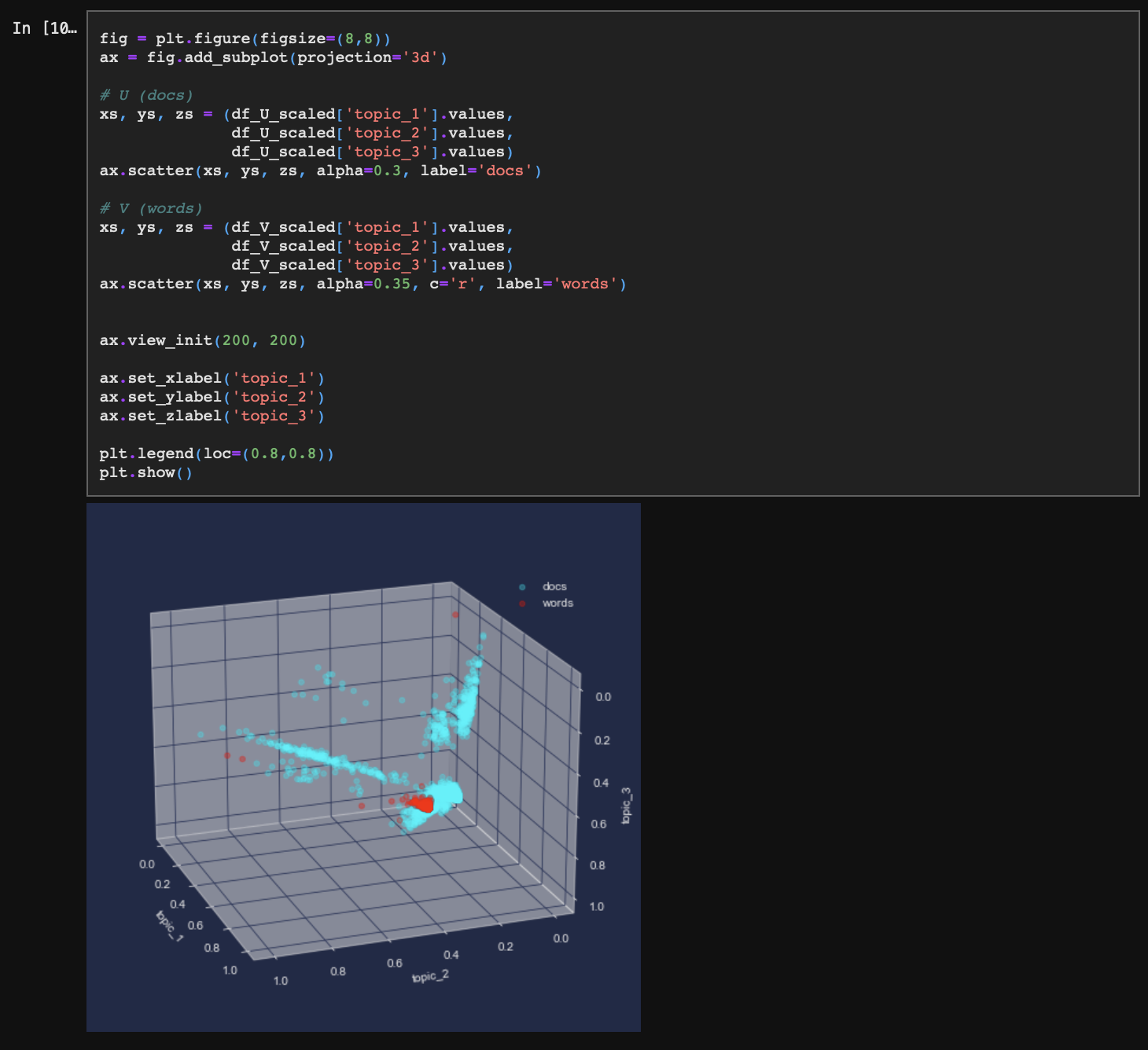
docs는 펼쳐져있는 반면, words는 상대적으로 공간상 수렴해 있다. 이 현상을 잠시 짚어보자.
Step 1로 돌아가서, 문서는 단어의 조합이라 했다. 각 단어는 동시 출현 빈도에 따라 연관성을 가지며 이러한 연관성이 결과적으로 토픽을 결정한다. 이렇게 결정된 토픽에 단어 조합으로 구성된 각 문서가 일치할 확률을 표현한다. 따라서 U와 V는 모두 토픽에 일치할 확률을 보여주지만 개념적으로 단어가 토픽의 정보량을 결정하고 그렇게 결정된 정보로 문서를 설명하기 때문에 words 대비 docs는 분포가 펼쳐질 수밖에 없다는 것이다.
Step 5. 토픽모델링 결과 분석
토픽모델링의 결과는 각 토픽별 단어의 확률분포, 문서의 확률분포가 되겠다. 즉, 특정 단어가 topic 1, 2, 3 각각에 해당할 확률이 얼마인지, 또 특정 문서가 topic 1, 2, 3 각각에 해당하는 확률이 얼마인지 확인할 수 있다. 우리가 앞서 뉴스 카테고리 1개를 선정 후, 카테고리 내 세부카테고리를 더 나눌 수 있는가? 에 관심을 가졌으며 토픽모델링 결과에 따라 그것의 여부를 확인하게 된다.
5-1. 각 토픽별 단어 분포
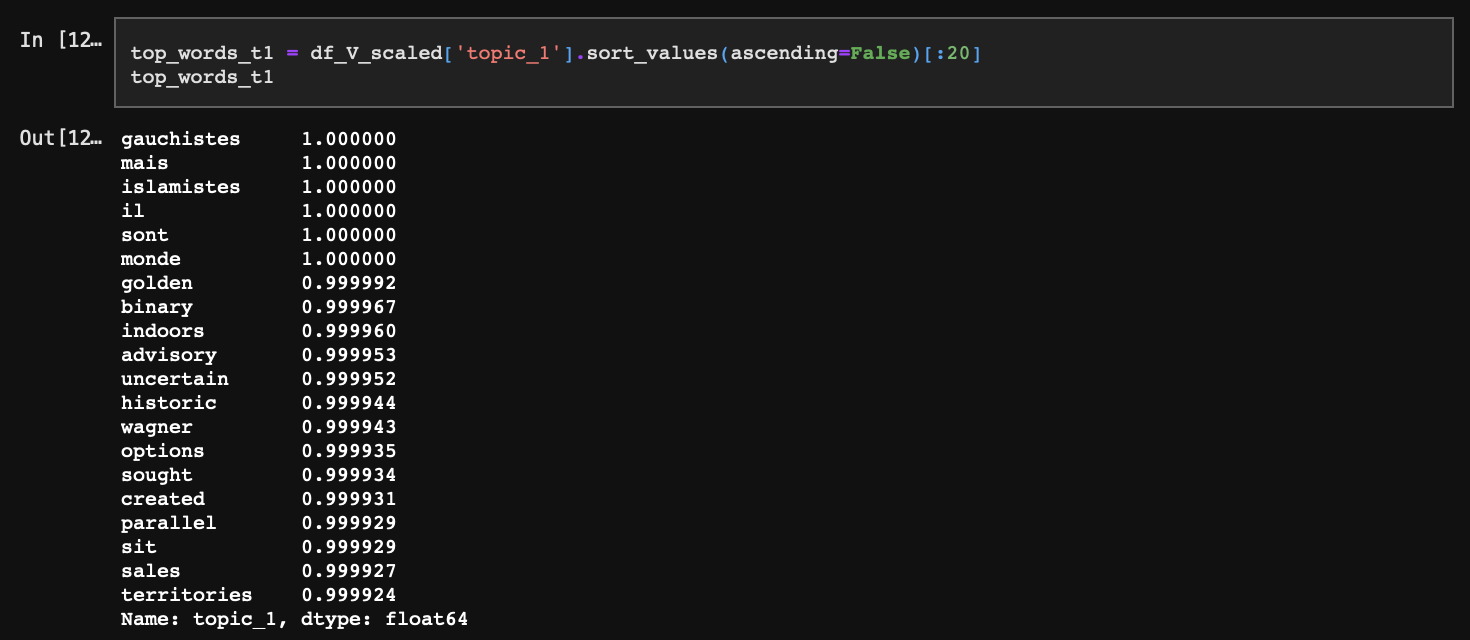
topic_1은 주로 무슬림계 범죄, 급진주의 테러리즘에 대한 내용으로 보인다. gauchistes(좌파), mais(이슬람 종교 협의회), islamistes(이슬람) 같은 단어들이 상단에 등장하고 있다.
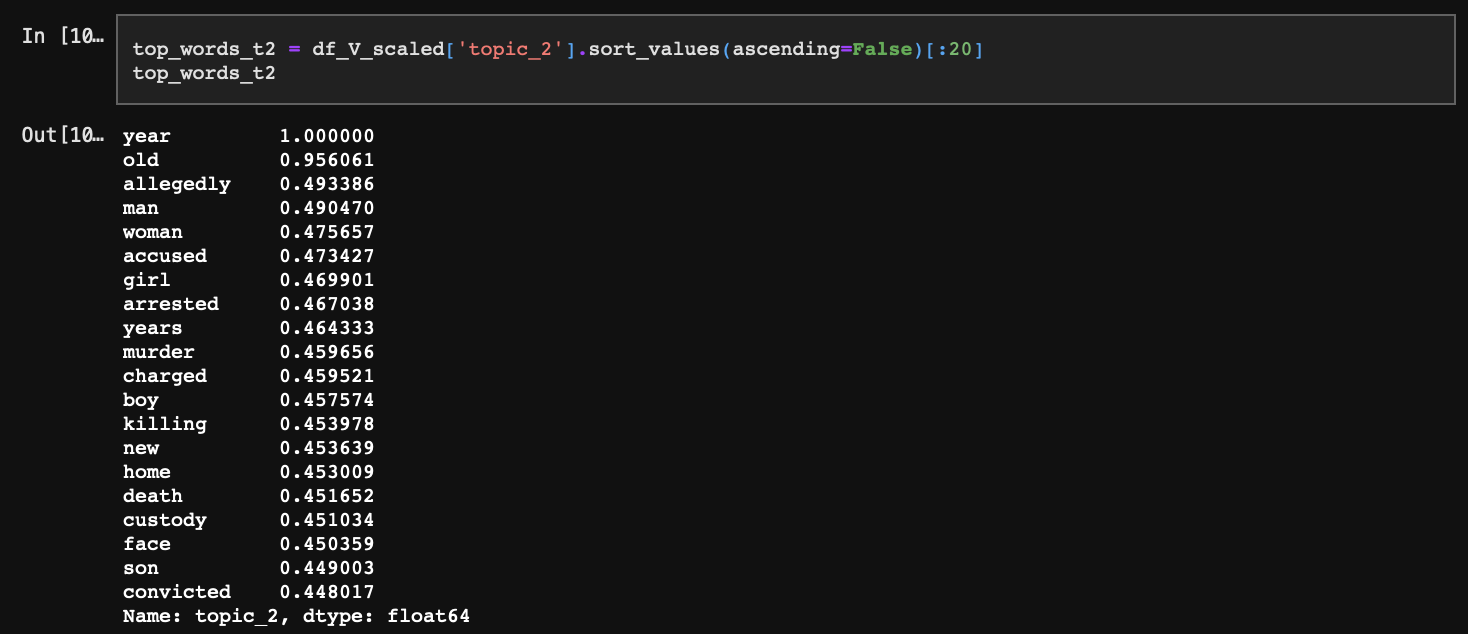
topic_2의 경우 남, 여, 아동 등 일반 시민 대상의 살인 범죄에 대한 내용으로 보이며 최상단에 year이라는 단어가 등장함으로 추측건대 연간 범죄율 등이 주축을 이룰 것이다.
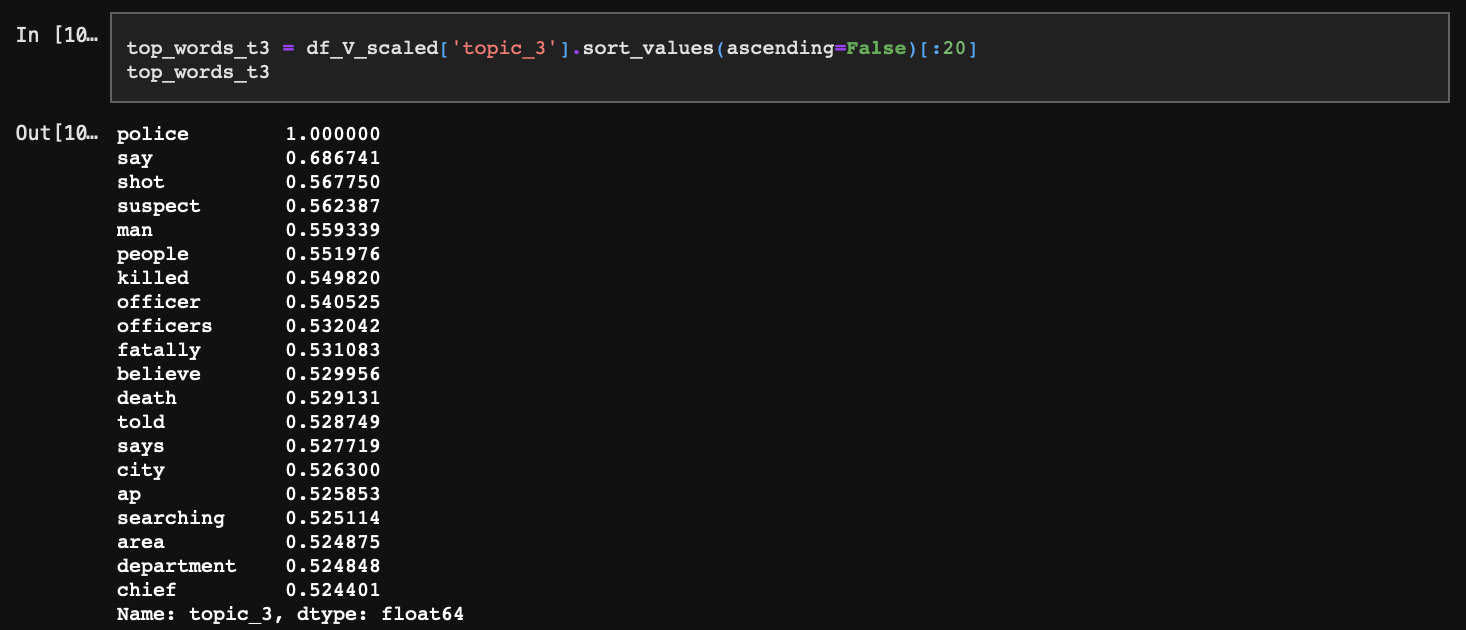
마지막으로 topic_3의 경우 police, officer, say 등이 상단에 위치한 것으로 보아 경찰의 행동이나 발언에 초점을 맞추고 있음을 알 수 있다.
종합적으로 topic_1는 테러 같은 국가적 이슈, topic_2는 소규모 범죄 피해, topic_3은 치안 및 관련 보도를 다루고 있으며, topic_1에 비해 topic_2와 topic_3은 그 성향이 상대적으로 뚜렷하지는 않다. 각 토픽에 대해 단어별 확률 분포를 시각적으로 확인해 보자.
topic_1의 경우 각 단어의 확률값이 전체적으로 매우 높은 반면, topic_2와 topic_3은 0.5 근처로 낮다. 이는 추출된 특이값 중 가장 앞에 위치해 있던 topic_1의 정보량이 가장 많기 때문이다.
한편으로는 토픽모델링을 수행했을 때 이렇게 모든 단어의 topic_1, topic_2, topic_3에 대한 각 확률값이 유사한 경우 제대로 된 분석 결과가 나오지 않는데, 이는 빈도기반 토픽모델링의 근본적 한계이기도 하다. 마지막 결론에서 이 내용에 대해 다시 언급하겠다.
5-2. 각 토픽별 문서 분포
다음으로 각 토픽과 가장 일치할 확률이 높은 문서도 확인해 볼 수 있다.
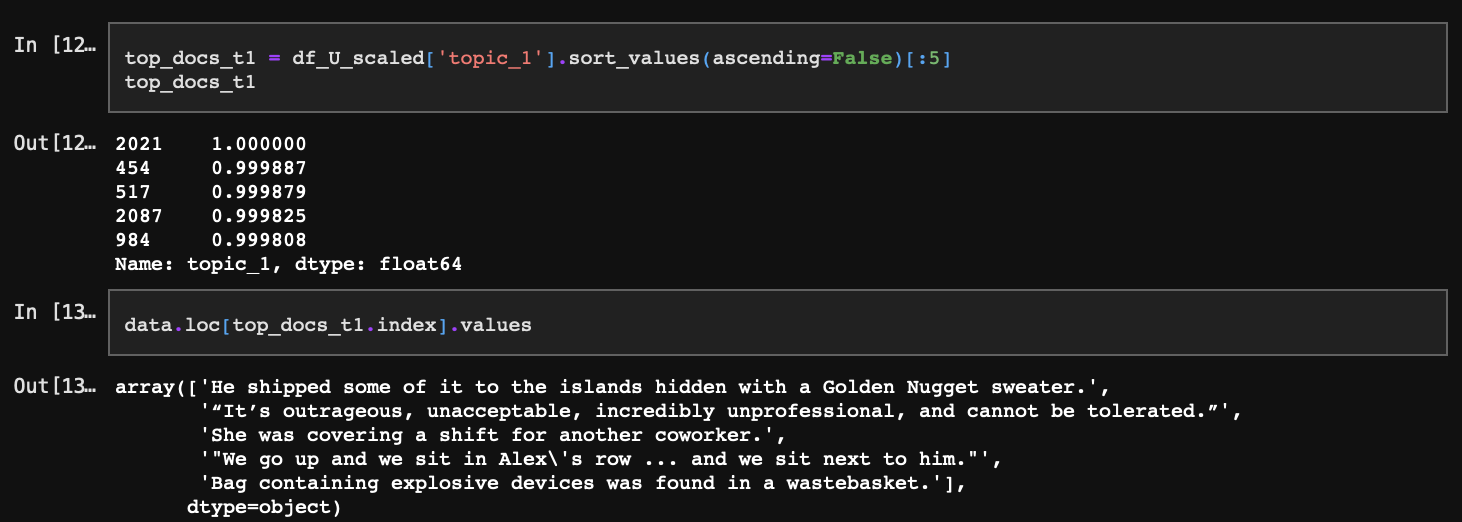
앞서 확인했을 때 topic_1은 테러와 같은 극단적인 범죄에 대한 토픽이었다. 위 문장 중 1번째는 밀수, 5번째는 폭탄테러에 대한 내용이며 나머지는 topic_1과 그다지 근접해 보이지는 않는다.
이러한 문서들도 포함된 이유는 topic_1과 일치할 단어의 확률 분포가 매우 높기 때문인데, 그러한 단어들이 문장에 조금만 들어가더라도 문장 자체의 토픽 일치 확률이 크게 상승하게 된다. 따라서 topic_1의 경우 확률 분포상 상위에 있는 문서들이 아이러니하게도 topic_1과 맥락상 유사하지 않을 가능성도 높은 것이다.
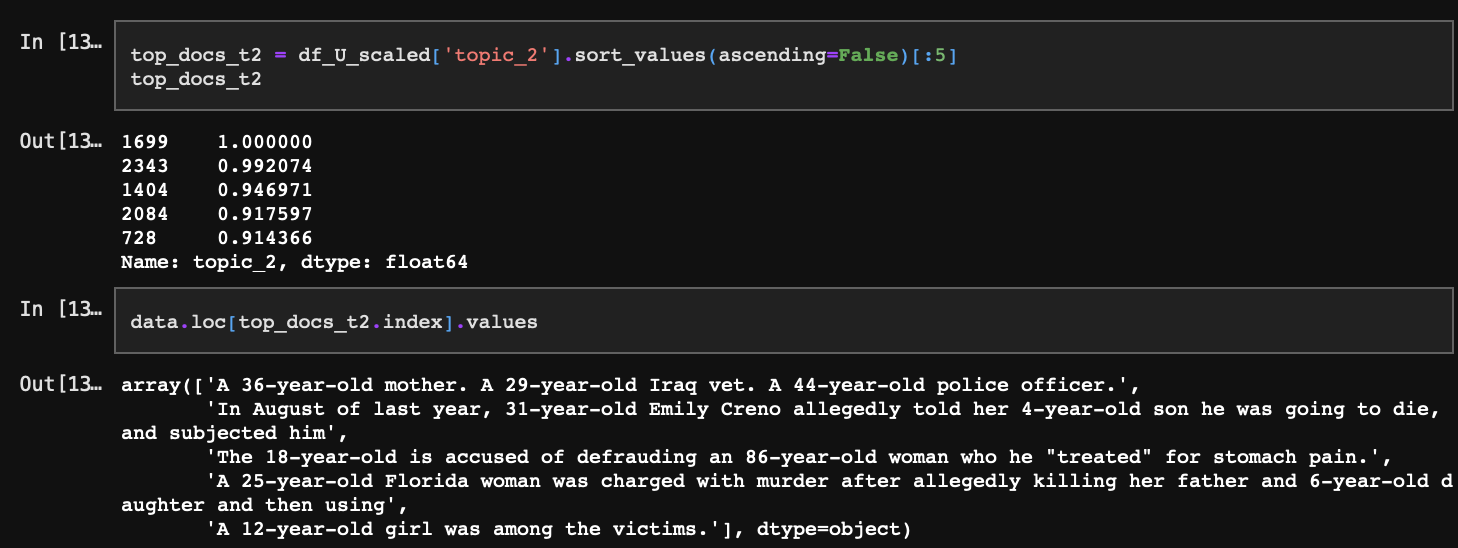
topic_2의 경우 상위 문서은 예상과 동일하게 일상에서 발생가능한 살인 범죄 등의 사건을 다루고 있다.
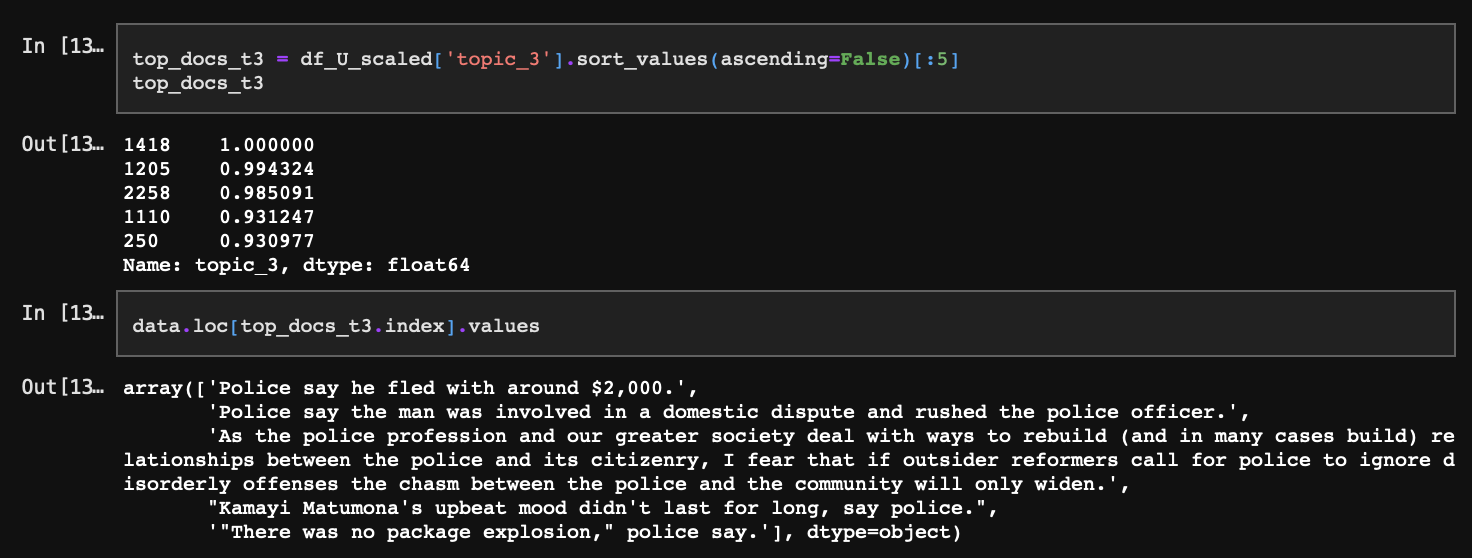
topic_3도 역시 마찬가지로 앞서 토픽에 대해 정의한 것처럼 경찰의 발언 및 보도에 관한 내용을 담고 있다.
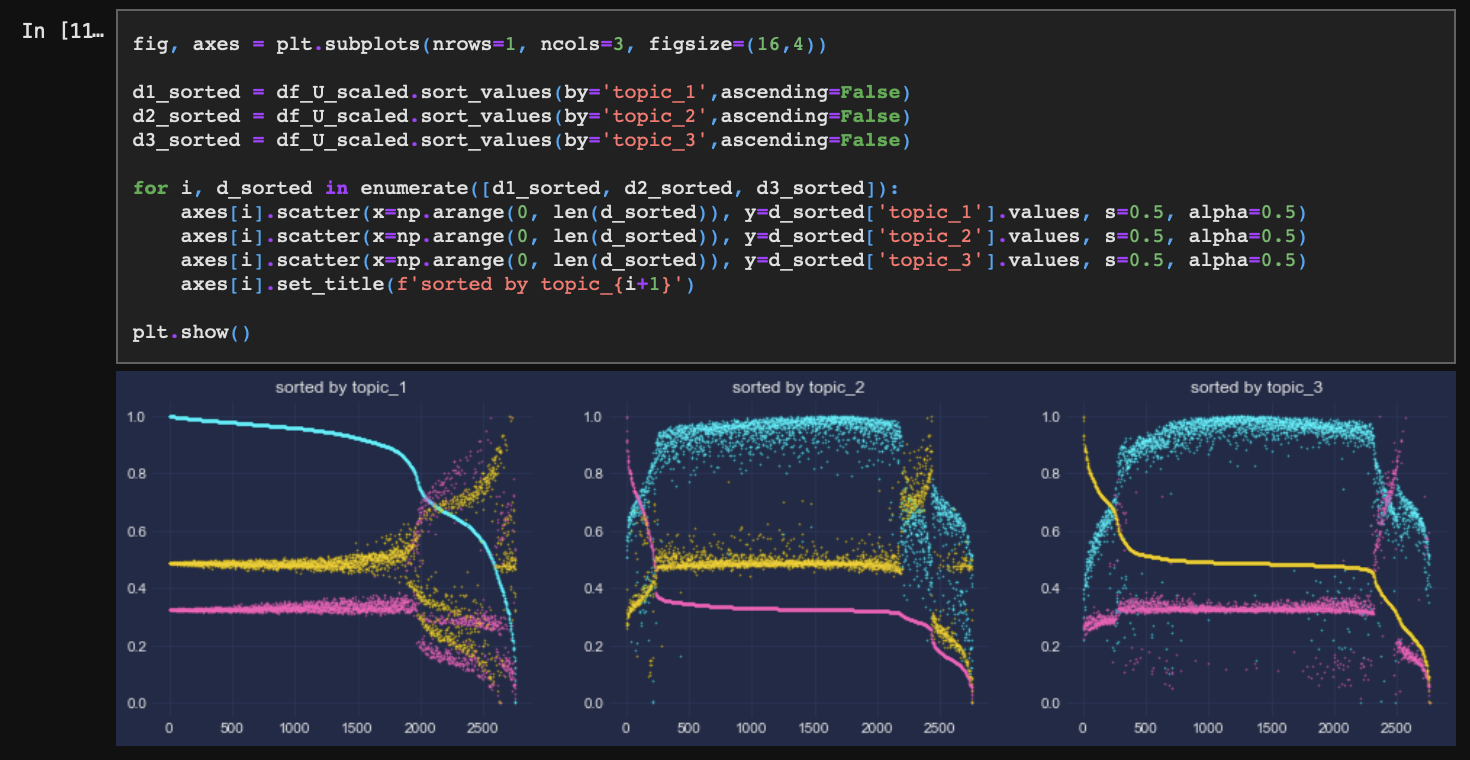
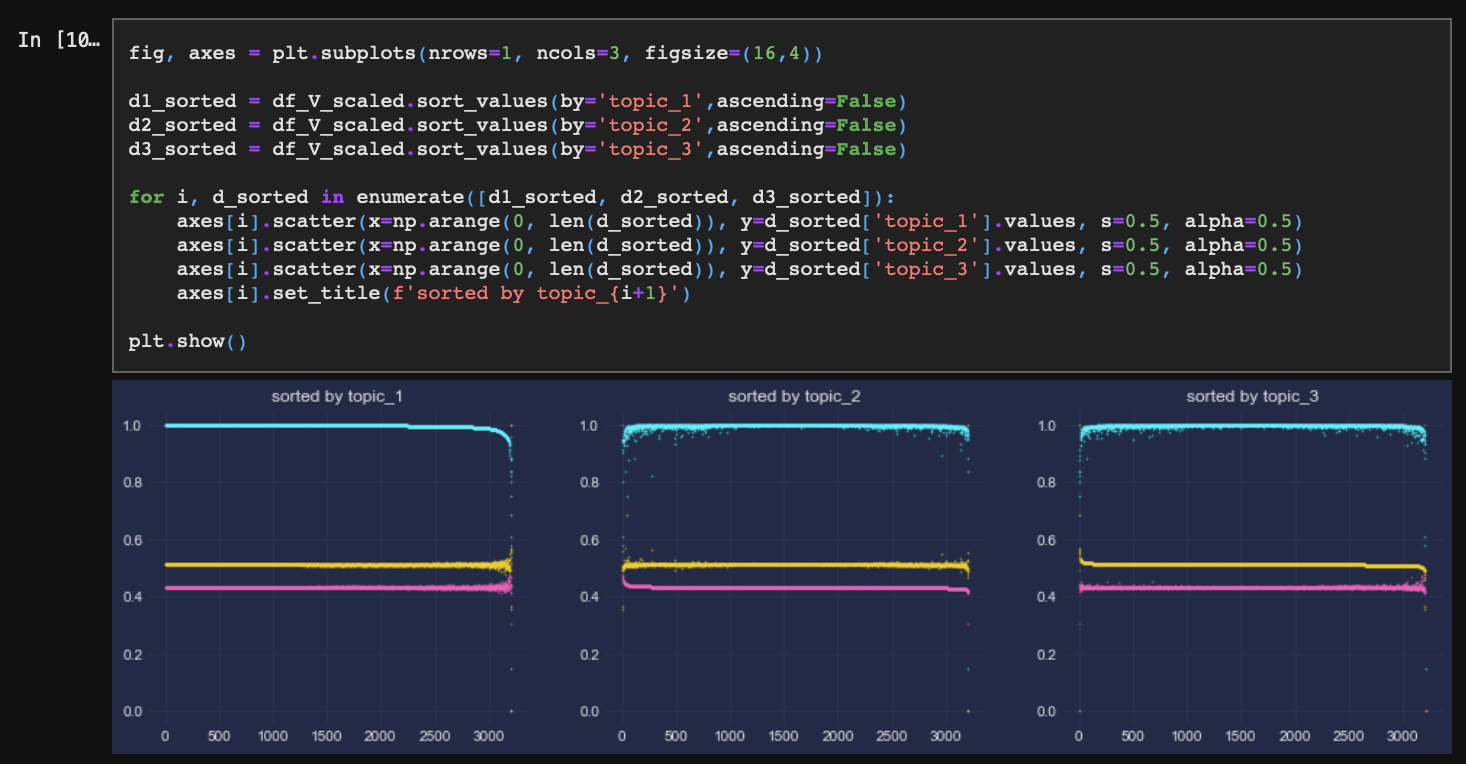
토픽별로 각각의 문서가 속할 확률을 보여주고 있으며 왼쪽부터 순서대로 topic_1, topic_2, topic_3을 기준으로 확률분포를 정렬시켰다.
문서의 기준으로 보면, 각 문서는 모두 3개 토픽에 포함될 확률을 각각 가지고 있는데, 약 2천 개의 문서는 모두 topic_1에 포함될 확률이 가장 높다.(가장 왼쪽 차트)
이는 앞에서도 확인했지만 topic_1과 일치하는 단어가 뚜렷한(확률이 큰) 만큼 그 단어가 속한 문서도 topic_1에 속할 확률이 높아지는 것에 원인이 있다.
5-3. 각 토픽별 주요 문서의 단어 분포
마지막으로 각 토픽별로 일치 확률이 가장 높은 문서들에 어떤 단어들이 포함되어 있는지 확인해 본다. 이때, 단어 역시 각 토픽별 가장 높은 확률을 가진 단어들로 구성하여 동일한 단어들이 문서별로 또 어떻게 다르게 분포되어 있는가를 확인하고자 한다.
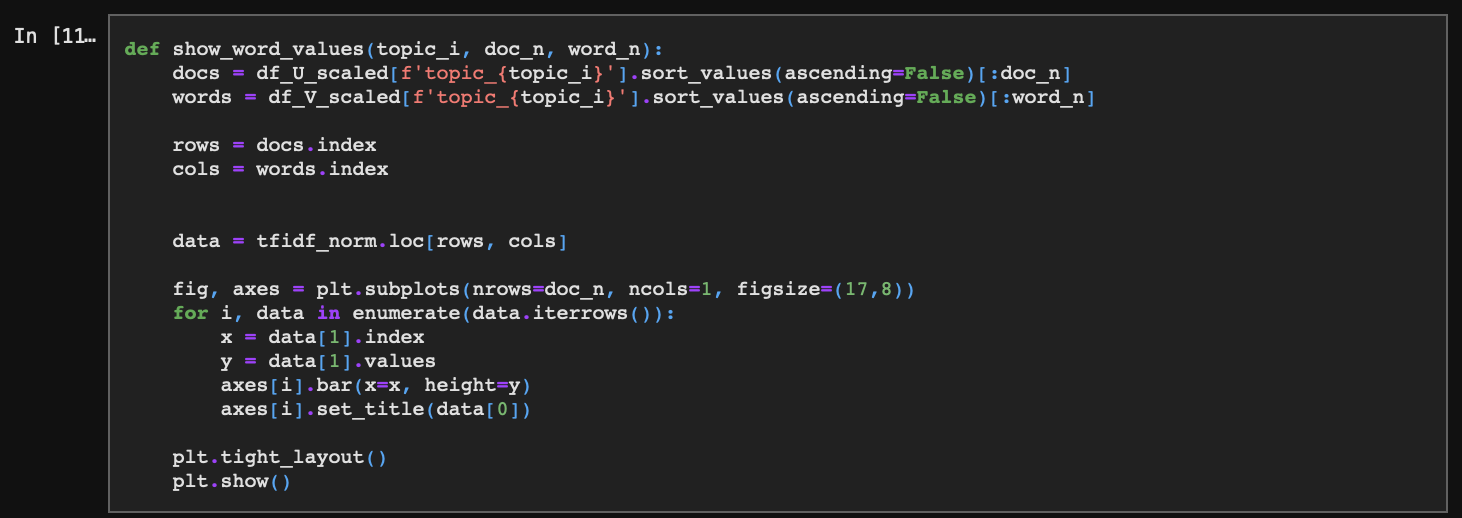
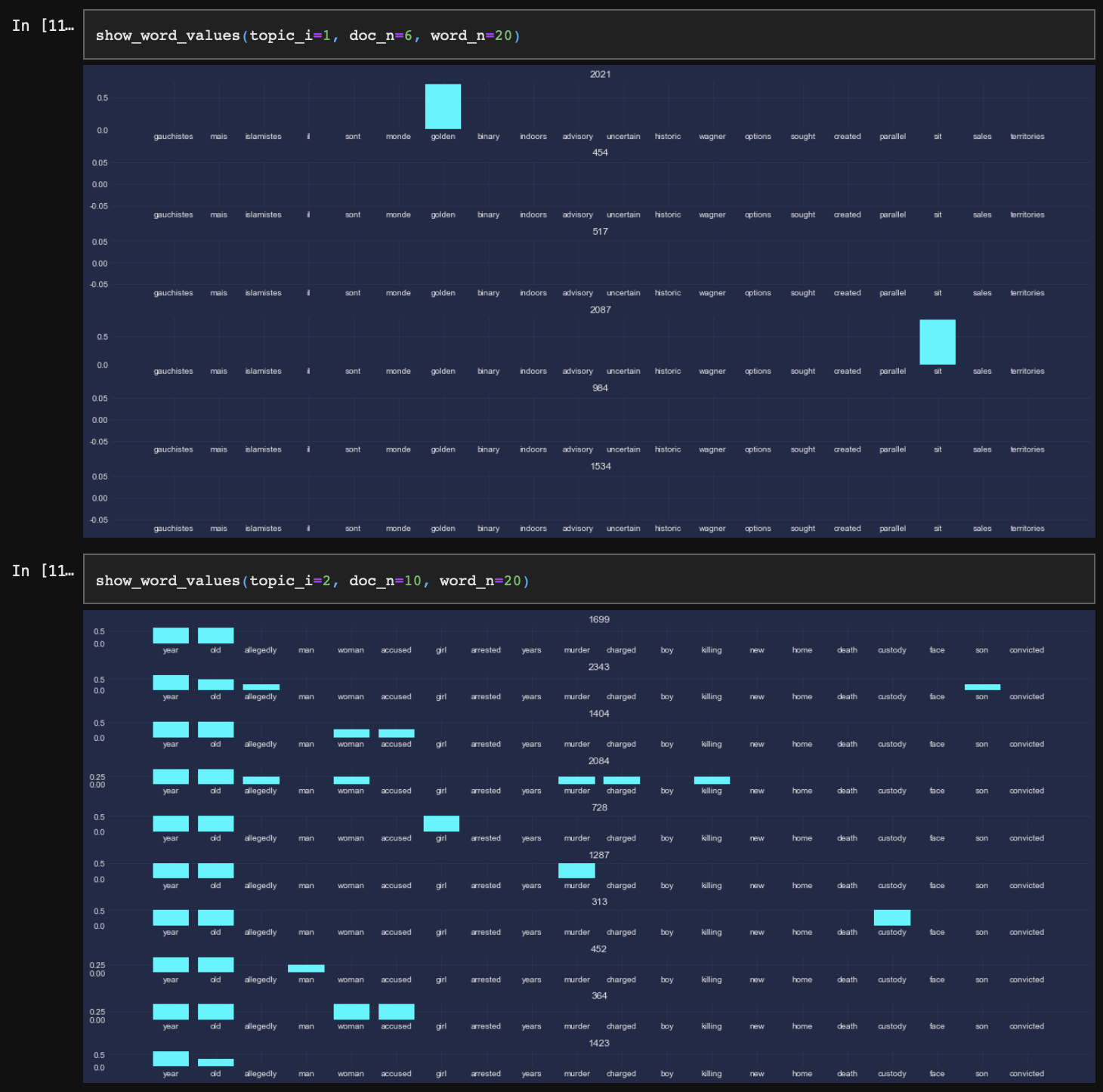
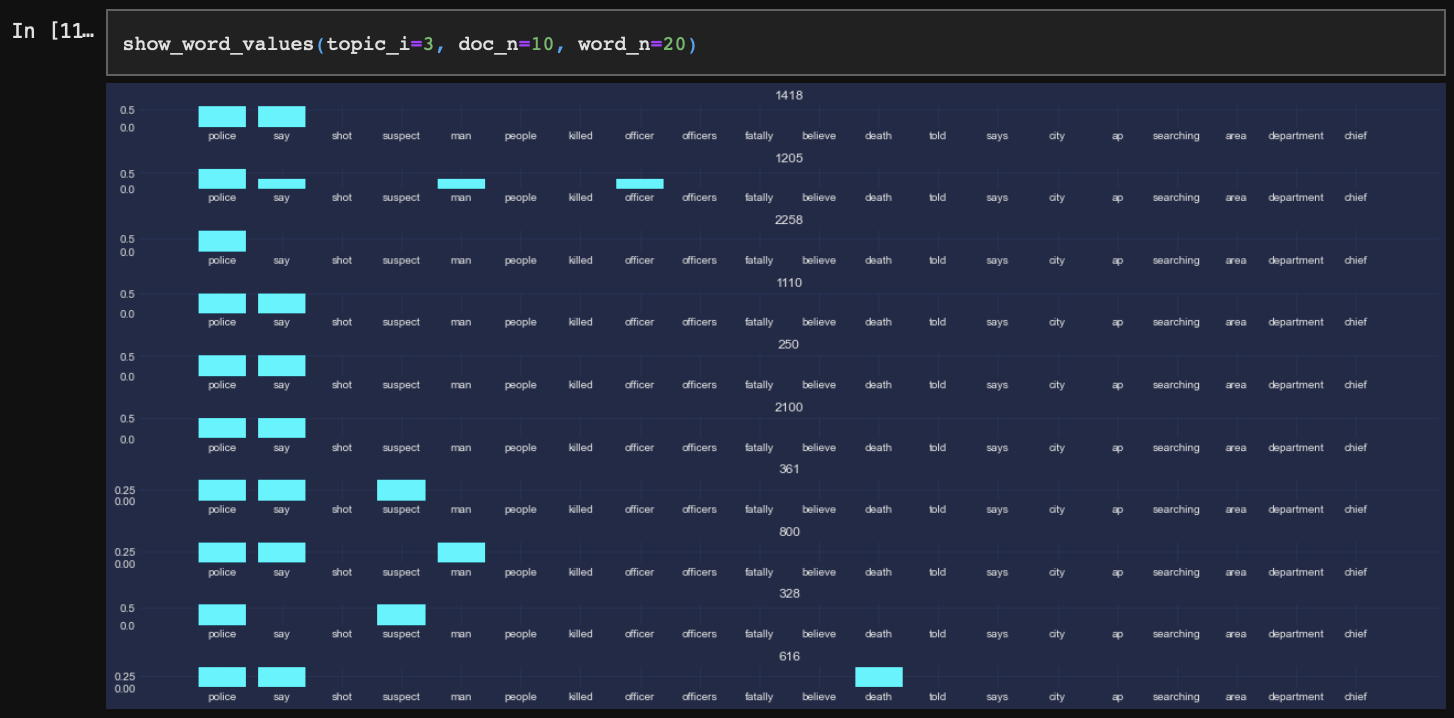
topic_2와 topic_3의 경우 각각의 문서가 토픽에 대한 확률값이 높은 단어들 위주로 잘 포함하고 있는 반면 topic_1은 그렇지 않다. 모든 단어들이 topic_1에 포함될 확률이 1에 근사하기 때문이다.
이렇게 문서별 단어 분포까지 확인해 보았다. 빈도기반 토픽모델링 LSA는 문장 내 단어의 동시 출현 빈도 및 특수성 가중치를 고려한 TF-IDF 행렬에 대해 특이값을 추출하는 방식으로 발전시켜 단어의 잠재 의미를 끌어내고자 시도했다는 점에서 의의가 있었다. 하지만 이 방법론의 결과로, 토픽 내부적으로는 연관관계가 높은 단어들이 서로 밀집할 수 있었으나 단어의 의미를 고려할 수 없다는 점에서 한계 또한 분명했다.
사실, 본 분석에서는 연산 속도 제약상 단어 집합이 정규분포를 따라야 한다는 LSA의 중요한 기본 가정을 무시하고 편향이 있는 단어 분포를 사용했다. 그러나 이를 차치하더라도 LSA는 그 원리상 빈도 기반 연관성만 고려하지 각 단어별 잠재된 의미를 고려하지는 않기 때문에 단어별로 각 토픽에 속할 확률이 큰 폭에서 차이가 없을 가능성이 매우 높으며, 분석에서는 그 특성을 다소 극대화해 보였다. 이러한 한계가 문서의 주제 분류에 있어서 현실적인 사용에 많은 제약을 주게 된다.