주식 시장의 난이도가 올라가면서 개인 투자자들도 자산 배분을 고려하고 있다. 자산 배분의 방식에는 여러 가지가 있겠지만 이번에는 미국과 한국 2개의 시장에만 투자하고, 각 시장에 대해 채권과 주식을 고르게 배분하는 전략으로 전개하고자 한다. 안전자산인 채권과 위험자산 주식을 어떤 비율로 분배하는 것이 가장 효율적일까?
Step 1. 야후 파이낸스 데이터 추출
Step 2. 일일 수익률 및 최종 수익률 확인
Step 3. 일일 수익률간 상관관계 시각화
Step 4. 변동성(위험) 대비 수익률 시각화
Step 5. 샤프 지수에 따른 포트폴리오 비율 시각화
Step 6. 사프 지수에 따른 포트폴리오 수익률 및 변동성 시각화
Step 7. 최적의 포트폴리오 비율Step 1. 야후 파이낸스 데이터 추출
데이터는 야후 파이낸스에서 가져올 것이므로 클래스를 미리 정의해두자.
class YFinance():
def __init__(self, tickers, period):
self.period = period
self.df_price = pd.DataFrame()
self.df_dividends = pd.DataFrame()
for ticker in tickers:
print(f'[INFO] 데이터 불러오는 중 .. (ticker : {ticker})')
full_data = yf.Ticker(ticker).history(start=self.period[0], end=self.period[1])
self.df_price[ticker] = full_data['Close']
self.df_dividends[ticker] = full_data['Dividends']
time.sleep(0.5)
print(f'[INFO] 데이터셋 구성 완료')
def get_price(self):
return self.df_price
def get_dividends(self):
return self.df_dividends미국 주식은 S&P500 지수를, 한국 주식은 코스피 지수를 사용하며 채권은 각 국가의 7~10년물 국채 가격을 사용한다.
tickers = ['SPY', '^KS11','IEF', '148070.KS'] # 미국 주식, 한국 주식, 미국 채권, 한국 채권
start_date = '2012-02-28'
end_date = '2022-02-28'
y_finance = YFinance(tickers=tickers, period=(start_date, end_date))
yf_price = y_finance.get_price() # 주가
yf_dividends = y_finance.get_dividends() # 배당금
print('-------------------------------\n',yf_price.shape, yf_dividends.shape)
2012년 2월 28일부터 2022년 2월 28일 전까지 데이터를 불러왔지만 미국 장과 한국 장의 개장일이 다르기 때문에 데이터가 부족한 컬럼이 있을 수 있다. dropna()를 통해 한 컬럼이라도 데이터가 빠진 경우 행을 날려준다.
yf_price = yf_price.dropna()
yf_price.columns = ['us_stock','kr_stock','us_bond','kr_bond']
yf_dividends = yf_dividends.dropna()
yf_dividends.columns = yf_price.columns
print(yf_price.shape, yf_dividends.shape)
yf_price
현재 포트폴리오에서 배당금은 미국 주식(S&P500)과 미국 채권(7~10년물)에서만 발생했다. 이후 포트폴리오 수익률 계산에 사용할 예정이니 참고하자.
# 총 누적 배당금
yf_dividends.sum()
이렇게 가져온 데이터로 그래프를 한번 그려준다. 4개 티커 종가 범위가 모두 다르기 때문에 데이터가 시작되는 날짜를 기준일로 잡고 이후 증감에 대해 차트를 그린다.
price_rate = yf_price/yf_price.iloc[0] # 기준일(2012-02-28) 대비 증감
plt.figure(figsize=(12,4))
sns.lineplot(data=price_rate, linewidth=0.85)
plt.ylim((0, price_rate.max().max()))
plt.title('Increase/decrease rate compared to the base date')
plt.show()
Step 2. 일일 수익률, 최종 수익률 시각화
차트를 그렸으니 이번에는 일일 변동과 최종 수익률도 그래프로 그려보자. 일일 변동을 그려보면, 전체 기간 중 가격이 오른 날의 비중이 얼마나 되는지 확인할 수 있다.
plt.figure(figsize=(12,8))
pcc = yf_price.pct_change().iloc[1:,:] # 첫째 날 데이터 제거(NaN)
for i in range(4):
data = pcc.iloc[:,i]
plt.subplot(int(f'22{i+1}'))
sns.lineplot(data=data, linewidth=0.85, alpha=0.7)
inc_rate = (data > 0).sum() / len(data) * 100
plt.title(f'< {data.name} : Increase rate {inc_rate:.2f}% >')
plt.axhline(y=0, color='r', linestyle='--', linewidth=0.7, alpha=0.9)
plt.suptitle('Percent change of each asset')
plt.tight_layout()
plt.show()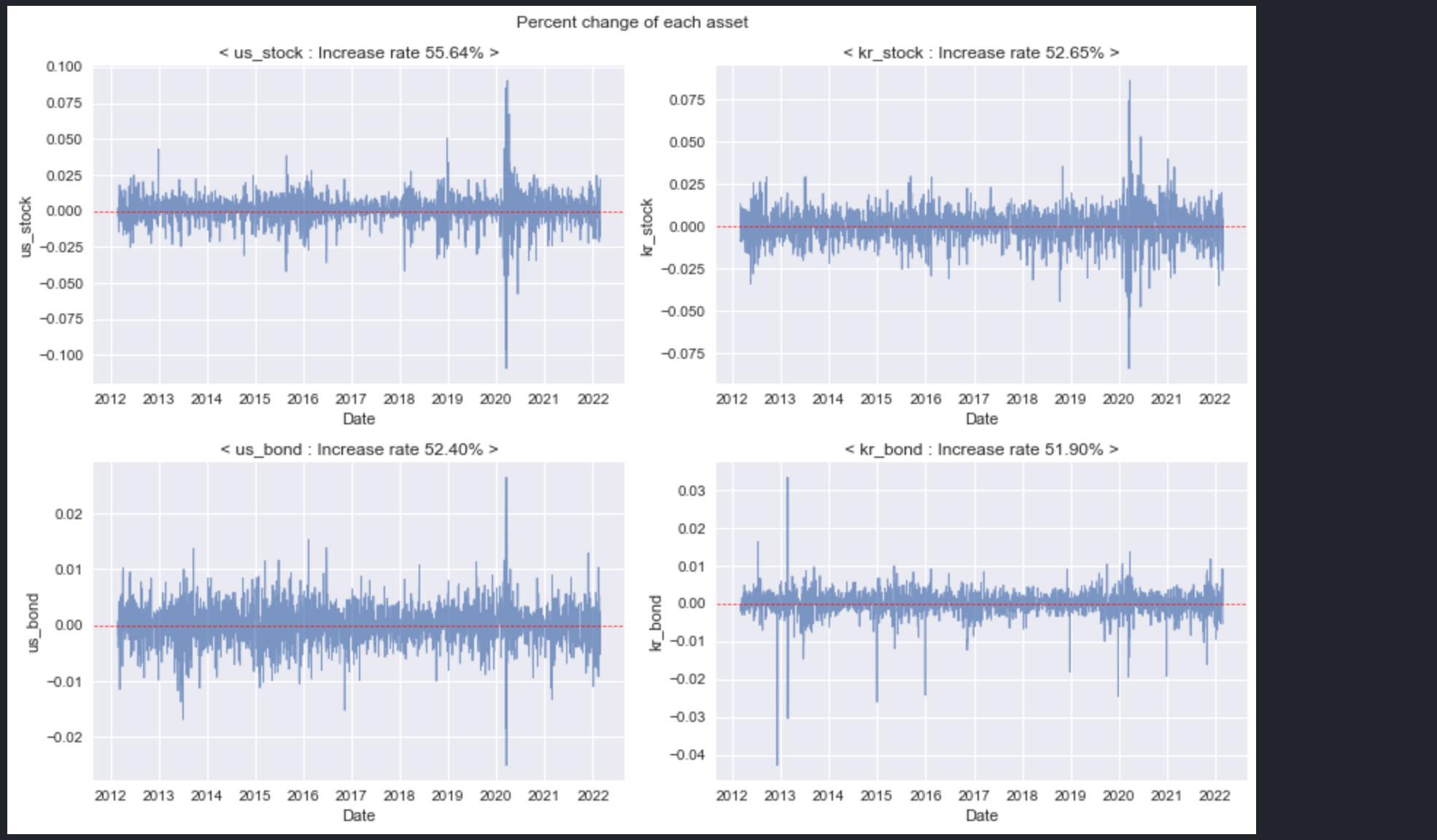
- S&P500의 경우, 2012년 2분기부터 2022년 1분기까지 전체 일수 중 55.64%가 상승했다.
- 코스피의 경우, 동기간 중 52.65%가 상승했다.
- 미국 국채의 경우, 동기간 중 52.4%가 상승했다.
- 한국 국채의 경우, 동기간 중 51.9%가 상승했다.
각 컬럼별로 최종 수익률도 살펴보자. 최종 수익률은 수집 기간의 첫째 날 대비 마지막 날이 몇 % 상승했는가를 확인하면 알 수 있다.
plt.figure(figsize=(9,4))
bars = sns.barplot(x=return_rate.index, y=return_rate.values, color='Blue', alpha=0.3)
for p in bars.patches:
bars.annotate(f'{p.get_height():.1f}%',
(p.get_x() + p.get_width() / 2., p.get_height()),
ha = 'center', va='center',
xytext = (0,9),
textcoords = 'offset points')
plt.title(f'Return rate of total period (%) - {(yf_price.index[-1] - yf_price.index[0]).days} days')
plt.show()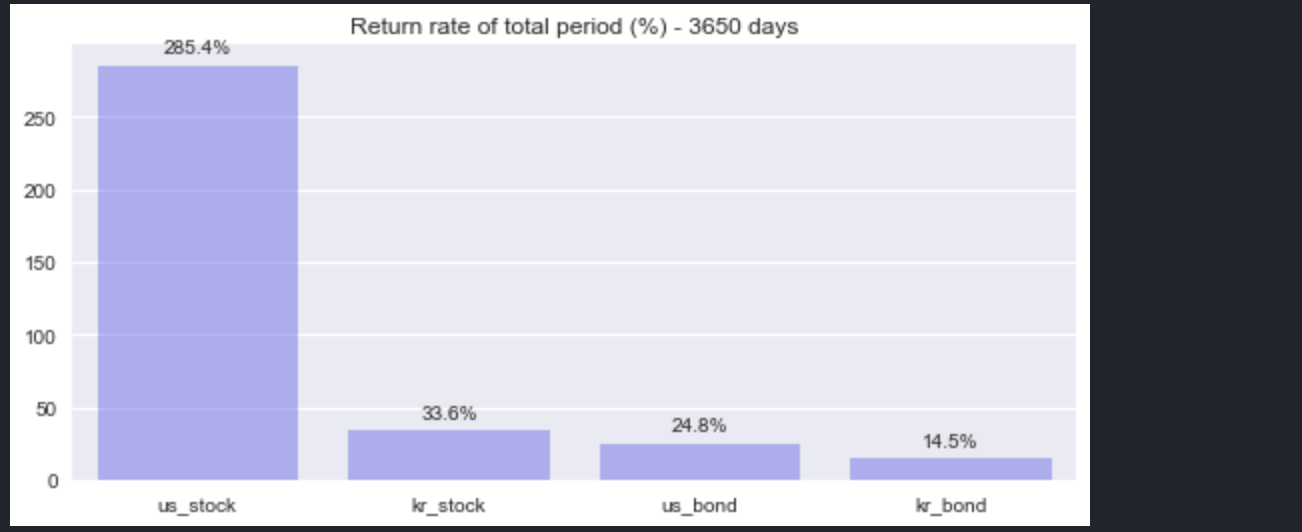
- S&P500의 경우, 관찰 기간 동안 285.4% 상승했다.
- 코스피의 경우, 관찰 기간 동안 33.6% 상승했다.
- 미국 국채 선물의 경우, 관찰 기간 동안 24.8% 상승했다.
- 한국 국채 선물의 경우, 관찰 기간 동안 14.5% 상승했다.
Step 3. 일일 수익률 간 상관관계 시각화
포트폴리오를 꾸릴 때에는 상관관계가 낮은 자산들로 구성해야 한다. 수익률은 최대한 유지하면서 변동을 낮출 수 있기 때문이다. 아래 히트맵에 상관계수가 표시되어 있는데, 상관계수가 1에 가까울수록 같이 움직이는 자산이다. 가능하다면 상관계수가 0.2 이하의 낮은 수준으로 자산 조합을 선택하는 것이 좋다. 여기서는 미국 주식과 미국 국채, 한국 국채 3가지 조합이 좋아보인다. 한국 주식의 경우 미국 주식과 상관관계가 0.26으로, 포트폴리오 기준으로 고려할 때에는 다소 높은 편이다.
plt.title("Correlation of all asset's percent change")
sns.heatmap(yf_price.pct_change().corr(), cmap='Blues', linewidth=0.2, annot=True)
plt.show()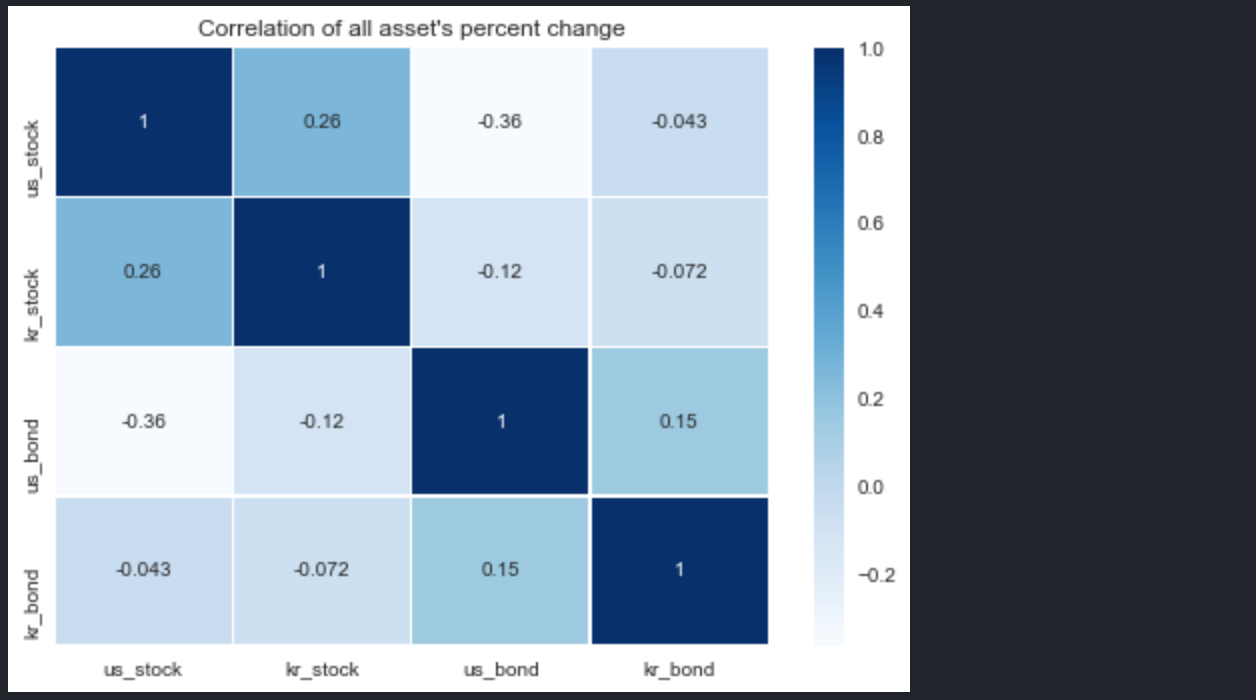
Step 4. 변동성(위험) 대비 수익률 시각화
미국 주식과 채권, 한국 주식과 채권 4가지 조합은 상관계수가 과하게 높은 케이스가 없기 때문에(미국 주식과 한국 주식 조합이 우려되긴 하지만) 포트폴리오로 고려해볼 수 있다. 이제는 포트폴리오 비중을 계산할 시간이다. 비중은 numpy random 함수를 통해 무작위로 총합 1이 되게 만들어주고, 1만 개의 비율 조합에 따른 연간 포트폴리오 리스크와 연평균 수익률을 계산하면 되겠다.
연 평균 수익률의 경우 전체 기간의 수익과 배당금을 합산한 금액을 첫날 자산 가격으로 나눠준 다음 10년의 기간에 대해 기하평균(10 제곱근)을 계산해주면 구할 수 있다. 복리 개념이기 때문에 단순 평균으로 계산하면 오차가 커진다.
연간 포트폴리오 리스크는 연간 수익률의 공분산을 구한 다음 '포트폴리오 비율의 역행렬 x 공분산 x 포트폴리오 비율'을 계산하면 포트폴리오 분산(변동성 제곱)이 나오는데, 루트를 씌워 표준편차(변동성)로 만들어주면 된다.
import numpy as np
port_ratios = []
port_returns = np.array([])
port_risks = np.array([])
for i in range(10000): # 포트폴리오 비율 조합 10000개
# 포트폴리오 비율
port_ratio = np.random.rand(len(yf_price.columns)) # 4가지 랜덤 실수 조합
port_ratio /= port_ratio.sum() # 합계가 1인 랜덤 실수
port_ratios.append(port_ratio)
# 연 평균 수익률
total_return_rate = (yf_price.iloc[-1] + yf_dividends.sum()) / yf_price.iloc[0] # 배당금 합산 총 수익률(%)
annual_avg_rr = total_return_rate ** (1/10) # 연 (기하)평균 수익률(%)
port_return = np.dot(port_ratio, annual_avg_rr-1) # 연 평균 포트폴리오 수익률 = 연 평균 수익률과 포트폴리오 비율의 행렬곱
port_returns = np.append(port_returns, port_return)
# 연간 리스크
annual_cov = yf_price.pct_change().cov() * len(yf_price)/10 # 연간 수익률의 공분산 = 일별 수익률 공분산 * 연간 평균 거래일수
port_risk = np.sqrt(np.dot(port_ratio.T, np.dot(annual_cov, port_ratio))) # E(Volatility) = sqrt(WT*COV*W)
port_risks = np.append(port_risks, port_risk)위 식이 돌면, 1만 개의 포트폴리오 비율 조합과 각 포트폴리오 비율에 따른 연 평균 수익률과 연간 리스크가 계산된다.
여기서 구한 연 평균 수익률을 연간 리스크로 나눠주면 샤프지수의 근사치(*샤프지수는 '(포트폴리오 수익률-시장 수익률)/(포트폴리오 리스크)'로 계산되는데, 여기서는 순위만 매기면 되기 때문에 시장 수익률을 빼는 과정이 생략되어 있다. 이 때문에 근사치라 표현했다.)가 나온다. 샤프지수는 공식에서 알 수 있듯이 단위 위험(편차, 변동성) 당 수익률로, 감수하는 리스크 대비 기대 수익이 얼마나 되는가를 표현한다. 포트폴리오의 효율성을 판단하는 데에 유용하게 쓰이는 지표다.
아래 차트는 1만개의 무작위 포트폴리오를 리스크 대비 수익률로 보여주고 있다. 그중에서 샤프지수가 가장 높은 것과 변동성이 가장 낮은 것을 각각 빨간색 삼각형, 파란색 삼각형으로 표시해줬다.
sorted_shape_idx = np.argsort(port_returns/port_risks)
sorted_risk_idx = np.argsort(port_risks)plt.figure(figsize=(12,6))
sns.scatterplot(x=port_risks, y=port_returns, c=port_returns/port_risks, cmap='cool', alpha=0.85, s=20)
sns.scatterplot(x=port_risks[sorted_shape_idx[-1:]], y=port_returns[sorted_shape_idx[-1:]], color='r', marker='^', s=500)
sns.scatterplot(x=port_risks[sorted_risk_idx[:1]], y=port_returns[sorted_risk_idx[:1]], color='b', marker='v', s=500)
plt.title('Return per unit risk')
plt.show()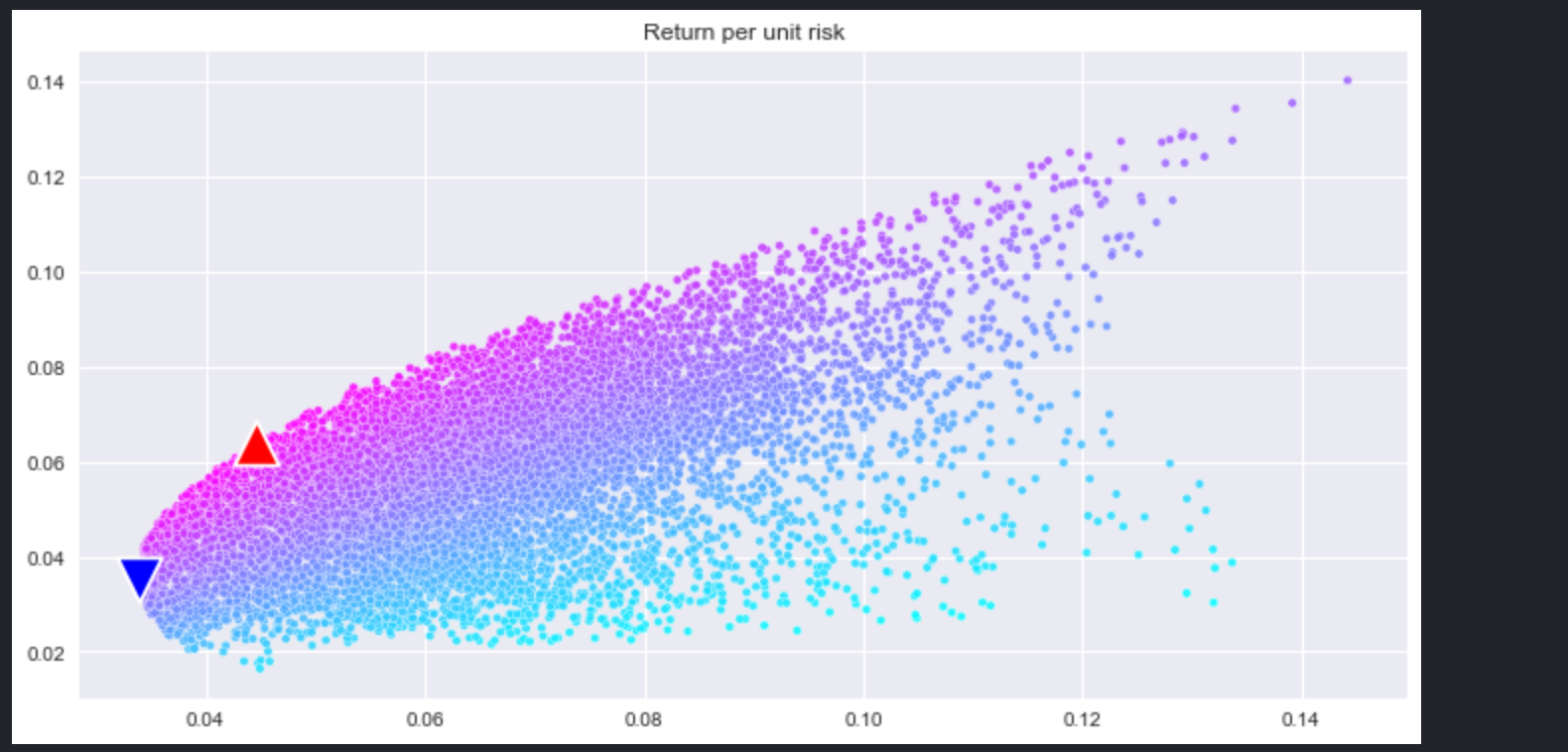
Step 5. 샤프 지수에 따른 포트폴리오 비율 시각화
이번에는 샤프 지수가 가장 높은 포트폴리오부터 가장 낮은 포트폴리오까지 샤프 지수 순으로 나열해서 보여줄 것인데, 포트폴리오에서 각 자산이 차지하는 비율을 색상으로 표현한다.
port_df = pd.DataFrame(port_ratios)
sorted_port_df = port_df.iloc[sorted_shape_idx[::-1]] # 역순
sorted_port_df.columns = yf_price.columns
plt.figure(figsize=(12,4))
plt.stackplot(np.arange(1,len(sorted_port_df)+1,1), np.array(sorted_port_df.T), labels=sorted_port_df.columns)
plt.xlim(0,10000)
plt.legend(bbox_to_anchor=(1.12,0.95))
plt.xlabel('Ranking of Sharpe Ratio')
plt.ylabel('Portfolio Ratio')
plt.title('Ranking of Optimal Portfolios by Sharpe Ratio')
plt.show()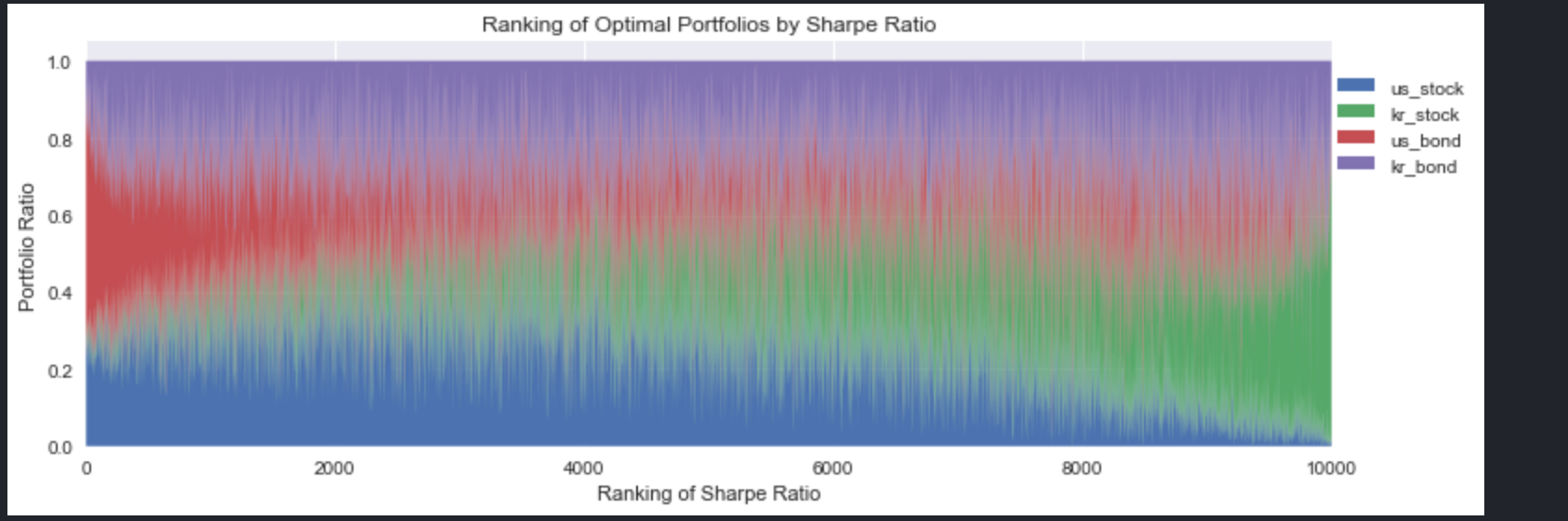
왼쪽으로 갈수록 샤프지수가 가장 높은 포트폴리오다. 샤프지수가 높을수록 미국 채권의 비중이 높아지고, 한국 주식 비중은 낮아지는 것을 알 수 있다. 한국 국채와 미국 주식의 비중은 남는 포지션에 적절히 배분하는 것이 좋겠다.
Step 6. 샤프 지수에 따른 포트폴리오 수익률 및 변동성 시각화
포트폴리오의 샤프지수가 높을 수록 수익률과 변동성이 어떤지 눈으로 확인하고 싶다. 따라서 같은 X축(샤프지수 내림차순)을 놓고 수익률과 변동성을 y축으로 그려본다.
sorted_returns = port_returns[[sorted_port_df.index]]
sorted_risks = port_risks[[sorted_port_df.index]]
plt.figure(figsize=(12,4))
plt.fill_between(x=np.arange(1,len(sorted_returns)+1,1), y1=sorted_returns.tolist(), label='return')
plt.fill_between(x=np.arange(1,len(sorted_risks)+1,1), y1=sorted_risks.tolist(), alpha=0.3, label='risk')
plt.xlabel('Ranking of Sharpe Ratio')
plt.ylabel('Return & Risk')
plt.title('Returns & Risks of Portfolio by Sharpe Ratio Ranking')
plt.legend()
plt.show()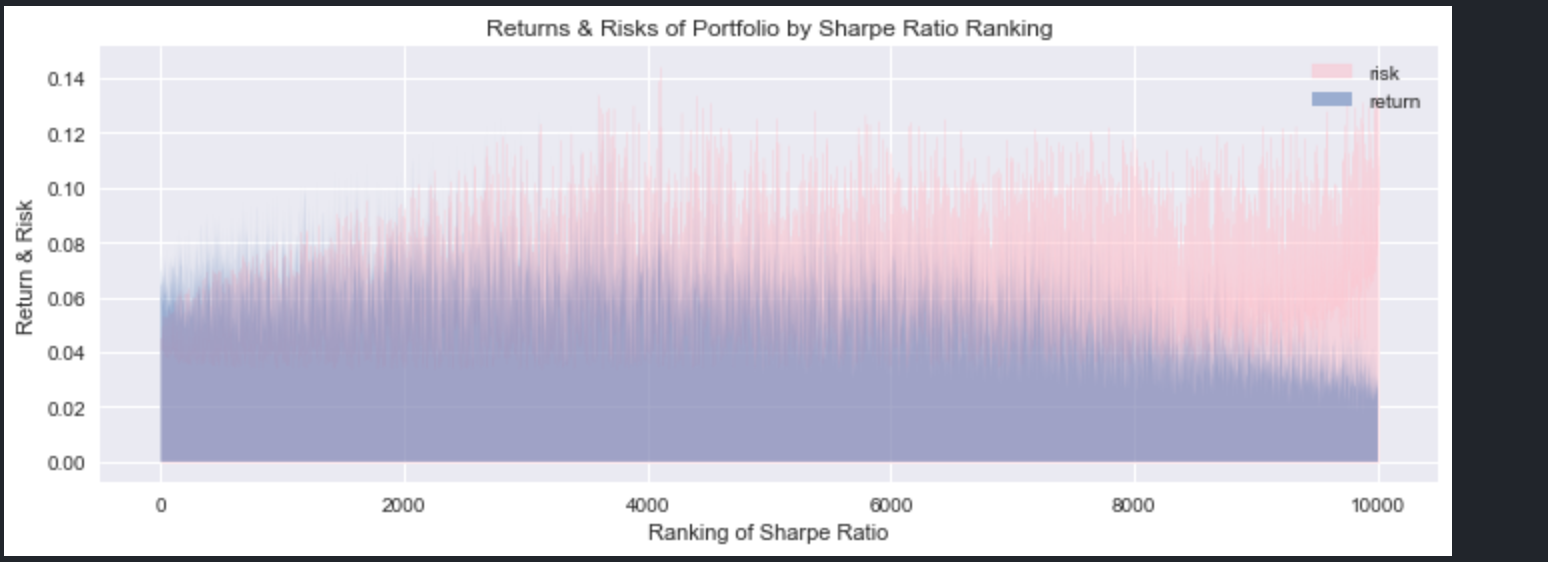
샤프지수가 높을 수록 수익률은 높아지고, 변동성은 낮아지는 경향을 보인다.
Step 7. 최적의 포트폴리오 비율
그래서 만약 미국 국채와 주식, 그리고 한국 국채와 주식으로 포트폴리오를 구성한다면, 2012년 2분기부터 2022년 1분기까지의 수익률 기록을 토대로 볼 때 아래의 비율이 최적의 포트폴리오가 된다.
print(f'최적의 포트폴리오 비율 : \n{pd.Series(sorted_port_df.iloc[0], index=sorted_port_df.columns)}')